Lilin
0%

基于前馈神经网络的姓氏分类

发表于 更新于 分类于
本文字数： 33k 阅读时长 ≈ 30 分钟

感知机

简介

感知机（英语：Perceptron）是Frank Rosenblatt在1957年就职于康奈尔航空实验室（Cornell Aeronautical Laboratory）时所发明的一种人工神经网络。它可以被视为一种最简单形式的前馈神经网络，是一种二元线性分类器。

Frank Rosenblatt给出了相应的感知机学习算法，常用的有感知机学习、最小二乘法和梯度下降法。譬如，感知机利用梯度下降法对损失函数进行极小化，求出可将训练数据进行线性划分的分离超平面，从而求得感知机模型。

感知机是生物神经细胞的简单抽象。神经细胞结构大致可分为：树突、突触、细胞体及轴突。单个神经细胞可被视为一种只有两种状态的机器——激活时为‘是’，而未激活时为‘否’。神经细胞的状态取决于从其它的神经细胞收到的输入信号量，及突触的强度（抑制或加强）。当信号量总和超过了某个阈值时，细胞体就会激活，产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。为了模拟神经细胞行为，与之对应的感知机基础概念被提出，如权量（突触）、偏置（阈值）及激活函数（细胞体）。

在人工神经网络领域中，感知机也被指为单层的人工神经网络，以区别于较复杂的多层感知机（Multilayer Perceptron）。作为一种线性分类器，（单层）感知机可说是最简单的前向人工神经网络形式。尽管结构简单，感知机能够学习并解决相当复杂的问题。感知机主要的本质缺陷是它不能处理线性不可分问题。

单层感知机

模型结构

单层感知机的模型可以简单表示为：
$$ f(x) = sign(w*x+b) $$
对于具有 $n$ 个输入 $x_{i}$ 以及对应连接权重系数为 $w_j$ 的感知机，首先通过线性加权得到输入数据的累加结果 $z$：$z=w_1 x_1+w_2 x_2+ … +b$。这里 $x_1,x_2,…,x_n$ 为感知机的输入，$w_1,w_2,…,w_n$为网络的权重系数，$b$ 为偏置项（$bias$）。然后将 $z$ 作为激活函数 $\varPhi(\cdot)$ 的输入，这里激活函数 $\varPhi(\cdot)$为 $sign$ 函数，其表达式为：

$$
sign(x) =
\begin{cases}
+1 \qquad & x \geq 0 \\
-1 \qquad & x \lt 0
\end{cases}
$$
$\varPhi(\cdot)$会将 $z$ 与某一阈值（此例中，阈值为$0$）进行比较，如果大于等于该阈值则感知器输出为 $1$，否则输出为 $-1$。通过这样的操作，输入数据被分类为 $1$ 或 $-1$ 这两个不同类别。
其结构为alt text

单层感知机存在的问题

alt text
单层感知机可被用来区分线性可分数据。在图中，逻辑与(AND)、逻辑与非(NAND)和逻辑或(OR)为线性可分函数，所以可利用单层感知机来模拟这些逻辑函数。但是，由于逻辑异或（XOR）是非线性可分的逻辑函数，因此单层感知机无法模拟逻辑异或函数的功能。

多层感知机

多层感知机的结构

由于无法模拟诸如异或以及其他复杂函数的功能，使得单层感知机的应用较为单一。一个简单的想法是，如果能在感知机模型中增加若干隐藏层，增强神经网络的非线性表达能力，就会让神经网络具有更强拟合能力。因此，由多个隐藏层构成的多层感知机被提出。

多层感知机由输入层、输出层和至少一层的隐藏层构成。网络中各个隐藏层中神经元可接收相邻前序隐藏层中所有神经元传递而来的信息，经过加工处理后将信息输出给相邻后续隐藏层中所有神经元。
alt text
在多层感知机中，相邻层所包含的神经元之间通常使用“全连接”方式进行连接。所谓“全连接”是指两个相邻层之间的神经元相互成对连接，但同一层内神经元之间没有连接。多层感知机可以模拟复杂非线性函数功能，所模拟函数的复杂性取决于网络隐藏层数目和各层中神经元数目。

隐藏层

我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。要做到这一点，最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出。 我们可以把前L-1层看作表示，把最后一层看作线性预测器。 这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP。 下面，我们以图的方式描述了多层感知机
alt text
这个多层感知机有4个输入，3个输出，其隐藏层包含5个隐藏单元。输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算。因此，这个多层感知机中的层数为2。注意，这两个层都是全连接的。每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。

激活函数

RELU函数

函数定义：

$$f(x)=\begin{cases} \begin{matrix} 0 & x<0 \end{matrix} \\ \begin{matrix} x & x\ge 0 \end{matrix} \end{cases}$$

导数：

$${ f }^{ ‘ }(x)=\begin{cases} \begin{matrix} 0 & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
函数图如图所示：
导函数图如图所示：alt text

sigmoid

函数定义：

$${ f }(x)=\sigma (x)=\frac { 1 }{ 1+{ e }^{ -x } } $$

导数：

$${ f }^{ ‘ }(x)=f(x)(1-f(x))$$
函数图形如图所示：alt text

导函数图如图所示：alt text
优点：

  1. $sigmoid$ 函数的输出映射在 $(0,1)$ 之间，单调连续，输出范围有限，优化稳定，可以用作输出层；
  2. 求导容易；

缺点：

  1. 由于其软饱和性，一旦落入饱和区梯度就会接近于0，根据反向传播的链式法则，容易产生梯度消失，导致训练出现问题；
  2. Sigmoid函数的输出恒大于0。非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢；
  3. 计算时，由于具有幂运算，计算复杂度较高，运算速度较慢。

tanh

函数定义：

$${ f }(x)=tanh(x)=\frac { { e }^{ x }-{ e }^{ -x } }{ { e }^{ x }+{ e }^{ -x } }$$

导数：

$${ f }^{ ‘ }(x)=1-f(x)^{ 2 }$$
函数图形如图所示：
alt text
导函数图如图所示：alt text
优点：

  1. $tanh$ 比 $sigmoid$ 函数收敛速度更快；
  2. 相比 $sigmoid$ 函数，$tanh$ 是以 $0$ 为中心的；

缺点：

  1. 与 $sigmoid$ 函数相同，由于饱和性容易产生的梯度消失；
  2. 与 $sigmoid$ 函数相同，由于具有幂运算，计算复杂度较高，运算速度较慢。

损失函数

均方差损失（Mean Square Error，MSE）

均方误差损失又称为二次损失、L2损失，常用于回归预测任务中。均方误差函数通过计算预测值和实际值之间距离（即误差）的平方来衡量模型优劣。即预测值和真实值越接近，两者的均方差就越小。

计算方式

假设有 $n$ 个训练数据 $x_i$，每个训练数据 $x_i$ 的真实输出为 $y_i$，模型对 $x_i$ 的预测值为 $\hat{y}_i$。该模型在 $n$ 个训练数据下所产生的均方误差损失可定义如下：

$$
MSE=\frac{1}{n}\sum_{i=1}^n{\left( y_i-\hat{y}_i \right) ^2}
$$
假设真实目标值为100，预测值在-10000到10000之间，我们绘制MSE函数曲线如图所示。可以看到，当预测值越接近100时，MSE损失值越小。MSE损失的范围为0到$\infty$ 。
alt text

交叉熵损失（cross-entropy loss ）

在物理学中，“熵”被用来表示热力学系统所呈现的无序程度。香农将这一概念引入信息论领域，提出了“信息熵”概念，通过对数函数来测量信息的不确定性。

交叉熵（cross entropy）是信息论中的重要概念，主要用来度量两个概率分布间的差异。假定 $p$ 和 $q$ 是数据 $x$ 的两个概率分布，通过 $q$ 来表示 $p$ 的交叉熵可如下计算：

$$
H\left( p,q \right) =-\sum_x{p\left( x \right) \log q\left( x \right)}
$$

交叉熵刻画了两个概率分布之间的距离，旨在描绘通过概率分布 $q$ 来表达概率分布 $p$ 的困难程度。根据公式不难理解，交叉熵越小，两个概率分布 $p$ 和 $q$ 越接近。

这里仍然以三类分类问题为例，假设数据 $x$ 属于类别 $1$。记数据x的类别分布概率为 $y$，显然 $y=(1,0,0)$代表数据 $x$ 的实际类别分布概率。记 $\hat{y}
$ 代表模型预测所得类别分布概率。

那么对于数据 $x$ 而言，其实际类别分布概率 $y$ 和模型预测类别分布概率 $\hat{y}$ 的交叉熵损失函数定义为：

$$
cross\ entropy=-y\times \log \left( \hat{y} \right)
$$

很显然，一个良好的神经网络要尽量保证对于每一个输入数据，神经网络所预测类别分布概率与实际类别分布概率之间的差距越小越好，即交叉熵越小越好。于是，可将交叉熵作为损失函数来训练神经网络。

三类分类问题中输入x的交叉熵损失示意图（x 属于第一类）

上图给出了一个三个类别分类的例子。由于输入数据 $x$ 属于类别 $1$，因此其实际类别概率分布值为 $y=(y_1,y_2,y_3)=(1,0,0)$。经过神经网络的变换，得到了输入数据 $x$ 相对于三个类别的预测中间值 $(z1,z2,z3)$。然后，经过 $Softmax$ 函数映射，得到神经网络所预测的输入数据 $x$ 的类别分布概率 $\hat{y}=\left( \hat{y}_1,\hat{y}_2,\hat{y}_3 \right)$。根据前面的介绍，$\hat{y}_1$、$\hat{y}_2$ 和 $\hat{y}_3$ 为 $(0,1)$ 范围之间的一个概率值。由于样本 $x$ 属于第一个类别，因此希望神经网络所预测得到的 $\hat{y}_1$取值要远远大于 $\hat{y}_2$ 和 $\hat{y}_3$ 的取值。为了得到这样的神经网络，在训练中可利用如下交叉熵损失函数来对模型参数进行优化：
$$
cross\ entropy=-\left( y_1\times \log \left( \hat{y}_1 \right) +y_2\times \log \left( \hat{y}_2 \right) +y_3\times \log \left( \hat{y}_3 \right) \right)
$$

在上式中，$y_2$ 和 $y_3$ 均为 $0$、$y_1$ 为 $1$，因此交叉熵损失函数简化为：
$$
-y_1\times \log \left( \hat{y}_1 \right) =-\log \left( \hat{y}_1 \right)
$$

在神经网络训练中，要将输入数据实际的类别概率分布与模型预测的类别概率分布之间的误差（即损失）从输出端向输入端传递，以便来优化模型参数。下面简单介绍根据交叉熵计算得到的误差从 $\hat{y}_1$ 传递给 $z_1$ 和 $z_2$（$z_3$ 的推导与 $z_2$ 相同）的情况。

$$
\frac{\partial \hat{y}_1}{\partial z_1}=\frac{\partial \left( \frac{e^{z_1}}{\sum_k{e^{z_k}}} \right)}{\partial z_1}=\frac{\left( e^{z_1} \right) ^{‘}\times \sum_k{e^{z_k}-e^{z_1}\times e^{z_1}}}{\left( \sum_k{e^{z_k}} \right) ^2}=\frac{e^{z_1}}{\sum_k{e^{z_k}}}-\frac{e^{z_1}}{\sum_k{e^{z_k}}}\times \frac{e^{z_1}}{\sum_k{e^{z_k}}}=\hat{y}_1\left( 1-\hat{y}_1 \right)
$$

由于交叉熵损失函数 $-\log \left( \hat{y}_1 \right)$ 对 $\hat{y}_1$ 求导的结果为 $-\frac{1}{\hat{y}_1}$，$\hat{y}_1\left( 1-\hat{y}_1 \right)$ 与 $-\frac{1}{\hat{y}_1}$ 相乘为 $\hat{y}_1-1$。这说明一旦得到模型预测输出 $\hat{y}_1$，将该输出减去1就是交叉损失函数相对于 $z_1$ 的偏导结果。

$$
\frac{\partial \hat{y}_1}{\partial z_2}=\frac{\partial \left( \frac{e^{z_1}}{\sum_k{e^{z_k}}} \right)}{\partial z_2}=\frac{0\times \sum_k{e^{z_k}-e^{z_1}\times e^{z_2}}}{\left( \sum_k{e^{z_k}} \right) ^2}=-\frac{e^{z_1}}{\sum_k{e^{z_k}}}\times \frac{e^{z_2}}{\sum_k{e^{z_k}}}=-\hat{y}_1\hat{y}_2
$$

同理，交叉熵损失函数导数为 $-\frac{1}{\hat{y}_1}$，$-\hat{y}_1\hat{y}_2$ 与 $-\frac{1}{\hat{y}_1}$ 相乘结果为 $\hat{y}_2$。这意味对于除第一个输出节点以外的节点进行偏导，在得到模型预测输出后，只要将其保存，就是交叉损失函数相对于其他节点的偏导结果。在 $z_1$、$z_2$ 和 $z_3$得到偏导结果后，再通过链式法则（后续介绍）将损失误差继续往输入端传递即可。

在上面的例子中，假设所预测中间值 $(z_1,z_2,z_3)$ 经过 $Softmax$ 映射后所得结果为 $(0.34,0.46,0.20)$。由于已知输入数据 $x$ 属于第一类，显然这个输出不理想而需要对模型参数进行优化。如果选择交叉熵损失函数来优化模型，则 $(z_1,z_2,z_3)$ 这一层的偏导值为 $(0.34-1,0.46,0.20)= (-0.66,0.46,0.20)$。

可以看出，$Softmax$ 和交叉熵损失函数相互结合，为偏导计算带来了极大便利。偏导计算使得损失误差从输出端向输入端传递，来对模型参数进行优化。在这里，交叉熵与$Softmax$ 函数结合在一起，因此也叫 $Softmax$ 损失（Softmax with cross-entropy loss）。

基于多层感知机的姓氏分类网络

我们将MLP应用于将姓氏分类到其原籍国的任务。从公开观察到的数据推断人口统计信息(如国籍)具有从产品推荐到确保不同人口统计用户获得公平结果的应用。人口统计和其他自我识别信息统称为“受保护属性”。“在建模和产品中使用这些属性时，必须小心。”我们首先对每个姓氏的字符进行拆分，并像对待“示例:将餐馆评论的情绪分类”中的单词一样对待它们。除了数据上的差异，字符层模型在结构和实现上与基于单词的模型基本相似.我们将通过描述姓氏分类器模型及其设计背后的思想过程来继续。

The Surname Dataset

姓氏数据集，它收集了来自18个不同国家的10,000个姓氏，这些姓氏是作者从互联网上不同的姓名来源收集的。该数据集将在本课程实验的几个示例中重用，并具有一些使其有趣的属性。第一个性质是它是相当不平衡的。排名前三的课程占数据的60%以上:27%是英语，21%是俄语，14%是阿拉伯语。剩下的15个民族的频率也在下降——这也是语言特有的特性。第二个特点是，在国籍和姓氏正字法(拼写)之间有一种有效和直观的关系。有些拼写变体与原籍国联系非常紧密(比如“O ‘Neill”、“Antonopoulos”、“Nagasawa”或“Zhu”)。

为了创建最终的数据集，我们从一个比课程补充材料中包含的版本处理更少的版本开始，并执行了几个数据集修改操作。第一个目的是减少这种不平衡——原始数据集中70%以上是俄文，这可能是由于抽样偏差或俄文姓氏的增多。为此，我们通过选择标记为俄语的姓氏的随机子集对这个过度代表的类进行子样本。接下来，我们根据国籍对数据集进行分组，并将数据集分为三个部分:70%到训练数据集，15%到验证数据集，最后15%到测试数据集，以便跨这些部分的类标签分布具有可比性。

SurnameDataset的实现与“Example: classification of Sentiment of Restaurant Reviews”中的ReviewDataset几乎相同，只是在getitem方法的实现方式上略有不同。回想一下，本课程中呈现的数据集类继承自PyTorch的数据集类，因此，我们需要实现两个函数:__getitem方法，它在给定索引时返回一个数据点;以及len方法，该方法返回数据集的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class SurnameDataset(Dataset):
    # Implementation is nearly identical to Section 3.5

    def __getitem__(self, index):
        """PyTorch 数据集的主要入口方法
        
        Args:
            index (int): 数据点的索引 
        Returns:
            一个包含数据点的字典:
                特征 (x_surname)
                标签 (y_nationality)
        """
        row = self._target_df.iloc[index]

        surname_vector = self._vectorizer.vectorize(row.surname)

        nationality_index = self._vectorizer.nationality_vocab.lookup_token(row.nationality)

        return {'x_surname': surname_vector,
                'y_nationality': nationality_index}

Vocabulary, Vectorizer, and DataLoader

为了使用字符对姓氏进行分类，我们使用词汇表、向量化器和DataLoader将姓氏字符串转换为向量化的minibatches。这些数据结构与“Example: Classifying Sentiment of Restaurant Reviews”中使用的数据结构相同，它们举例说明了一种多态性，这种多态性将姓氏的字符标记与Yelp评论的单词标记相同对待。数据不是通过将字令牌映射到整数来向量化的，而是通过将字符映射到整数来向量化的。

THE VOCABULARY CLASS

本例中使用的词汇类与“example: Classifying Sentiment of Restaurant Reviews”中的词汇完全相同，该词汇类将Yelp评论中的单词映射到对应的整数。简要概述一下，词汇表是两个Python字典的协调，这两个字典在令牌(在本例中是字符)和整数之间形成一个双射;也就是说，第一个字典将字符映射到整数索引，第二个字典将整数索引映射到字符。add_token方法用于向词汇表中添加新的令牌，lookup_token方法用于检索索引，lookup_index方法用于检索给定索引的令牌(在推断阶段很有用)。与Yelp评论的词汇表不同，我们使用的是one-hot词汇表，不计算字符出现的频率，只对频繁出现的条目进行限制。这主要是因为数据集很小，而且大多数字符足够频繁。

THE SURNAMEVECTORIZER

虽然词汇表将单个令牌(字符)转换为整数，但SurnameVectorizer负责应用词汇表并将姓氏转换为向量。实例化和使用非常类似于“示例:对餐馆评论的情绪进行分类”中的ReviewVectorizer，但有一个关键区别:字符串没有在空格上分割。姓氏是字符的序列，每个字符在我们的词汇表中是一个单独的标记。然而，在“卷积神经网络”出现之前，我们将忽略序列信息，通过迭代字符串输入中的每个字符来创建输入的收缩one-hot向量表示。我们为以前未遇到的字符指定一个特殊的令牌，即UNK。由于我们仅从训练数据实例化词汇表，而且验证或测试数据中可能有惟一的字符，所以在字符词汇表中仍然使用UNK符号。

虽然我们在这个示例中使用了收缩的one-hot，但是在后面的实验中，将了解其他向量化方法，它们是one-hot编码的替代方法，有时甚至更好。具体来说，在“示例:使用CNN对姓氏进行分类”中，将看到一个热门矩阵，其中每个字符都是矩阵中的一个位置，并具有自己的热门向量。然后，在实验5中，将学习嵌入层，返回整数向量的向量化，以及如何使用它们创建密集向量矩阵。看一下示例4-6中SurnameVectorizer的代码。

Example 4-6. Implementing SurnameVectorizer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class SurnameVectorizer(object):
    """协调词汇表并将它们应用到使用的向量化器"""
    def __init__(self, surname_vocab, nationality_vocab, max_surname_length):
        """
        参数:
            surname_vocab (Vocabulary): 将字符映射到整数的词汇表
            nationality_vocab (Vocabulary): 将国籍映射到整数的词汇表
            max_surname_length (int): 最长姓氏的长度
        """
        self.surname_vocab = surname_vocab
        self.nationality_vocab = nationality_vocab
        self._max_surname_length = max_surname_length

    def vectorize(self, surname):
        """
        参数:
            surname (str): 姓氏
        返回:
            one_hot_matrix (np.ndarray): 一个one-hot向量的矩阵
        """

        one_hot_matrix_size = (len(self.surname_vocab), self._max_surname_length)
        one_hot_matrix = np.zeros(one_hot_matrix_size, dtype=np.float32)
                               
        for position_index, character in enumerate(surname):
            character_index = self.surname_vocab.lookup_token(character)
            one_hot_matrix[character_index][position_index] = 1
        
        return one_hot_matrix

    @classmethod
    def from_dataframe(cls, surname_df):
        """从数据集DataFrame实例化向量化器
        
        参数:
            surname_df (pandas.DataFrame): 姓氏数据集
        返回:
            SurnameVectorizer的实例
        """
        surname_vocab = Vocabulary(unk_token="@")
        nationality_vocab = Vocabulary(add_unk=False)
        max_surname_length = 0

        for index, row in surname_df.iterrows():
            max_surname_length = max(max_surname_length, len(row.surname))
            for letter in row.surname:
                surname_vocab.add_token(letter)
            nationality_vocab.add_token(row.nationality)

        return cls(surname_vocab, nationality_vocab, max_surname_length)

The Surname Classifier Model

SurnameClassifier是本实验前面介绍的MLP的实现(示例4-7)。第一个线性层将输入向量映射到中间向量，并对该向量应用非线性。第二线性层将中间向量映射到预测向量。

在最后一步中，可选地应用softmax操作，以确保输出和为1;这就是所谓的“概率”。它是可选的原因与我们使用的损失函数的数学公式有关——交叉熵损失。我们研究了“损失函数”中的交叉熵损失。回想一下，交叉熵损失对于多类分类是最理想的，但是在训练过程中软最大值的计算不仅浪费而且在很多情况下并不稳定。

Example 4-7. The SurnameClassifier as an MLP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import torch.nn as nn
import torch.nn.functional as F

class SurnameClassifier(nn.Module):
    def __init__(self, initial_num_channels, num_classes, num_channels):
        """
        创建一个姓氏分类器。
        
        参数:
            initial_num_channels (int): 输入特征向量的大小
            num_classes (int): 输出预测向量的大小
            num_channels (int): 网络中要始终使用的恒定通道大小
        """
        super(SurnameClassifier, self).__init__()
        
        self.convnet = nn.Sequential(
            nn.Conv1d(in_channels=initial_num_channels, 
                      out_channels=num_channels, kernel_size=3),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels, 
                      kernel_size=3, stride=2),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels, 
                      kernel_size=3, stride=2),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels, 
                      kernel_size=3),
            nn.ELU()
        )
        self.fc = nn.Linear(num_channels, num_classes)

    def forward(self, x_surname, apply_softmax=False):
        """分类器的前向传播
        
        参数:
            x_surname (torch.Tensor): 输入数据张量。
                x_surname.shape 应为 (batch, initial_num_channels, max_surname_length)
            apply_softmax (bool): softmax 激活的标志
                如果与交叉熵损失一起使用，则应为 False
        返回:
            结果张量。tensor.shape 应为 (batch, num_classes)
        """
        features = self.convnet(x_surname).squeeze(dim=2)
       
        prediction_vector = self.fc(features)

        if apply_softmax:
            prediction_vector = F.softmax(prediction_vector, dim=1)

        return prediction_vector

The Training Routine

虽然我们使用了不同的模型、数据集和损失函数，但是训练例程是相同的。因此，在例4-8中，我们只展示了args以及本例中的训练例程与“示例:餐厅评论情绪分类”中的示例之间的主要区别。

Example 4-8. The args for classifying surnames with an MLP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
args = Namespace(
    # 数据和路径信息
    surname_csv="data/surnames/surnames_with_splits.csv",
    vectorizer_file="vectorizer.json",
    model_state_file="model.pth",
    save_dir="model_storage/ch4/cnn",
    # 模型超参数
    hidden_dim=100,
    num_channels=256,
    # 训练超参数
    seed=1337,
    learning_rate=0.001,
    batch_size=128,
    num_epochs=100,
    early_stopping_criteria=5,
    dropout_p=0.1,
    # 运行时选项
    cuda=False,
    reload_from_files=False,
    expand_filepaths_to_save_dir=True,
    catch_keyboard_interrupt=True
)

训练中最显著的差异与模型中输出的种类和使用的损失函数有关。在这个例子中，输出是一个多类预测向量，可以转换为概率。正如在模型描述中所描述的，这种输出的损失类型仅限于CrossEntropyLoss和NLLLoss。由于它的简化，我们使用了CrossEntropyLoss。

在例4-9中，我们展示了数据集、模型、损失函数和优化器的实例化。这些实例应该看起来与“示例:将餐馆评论的情绪分类”中的实例几乎相同。事实上，在本课程后面的实验中，这种模式将对每个示例进行重复。

Example 4-9. Instantiating the dataset, model, loss, and optimizer

1
2
3
4
5
6
7
8
9
10
11
dataset = SurnameDataset.load_dataset_and_make_vectorizer(args.surname_csv)
vectorizer = dataset.get_vectorizer()

classifier = SurnameClassifier(input_dim=len(vectorizer.surname_vocab),
                               hidden_dim=args.hidden_dim,
                               output_dim=len(vectorizer.nationality_vocab))

classifier = classifier.to(args.device)    

loss_func = nn.CrossEntropyLoss(dataset.class_weights)
optimizer = optim.Adam(classifier.parameters(), lr=args.learning_rate)

THE TRAINING LOOP

与“Example: Classifying Sentiment of Restaurant Reviews”中的训练循环相比，本例的训练循环除了变量名以外几乎是相同的。具体来说，示例4-10显示了使用不同的key从batch_dict中获取数据。除了外观上的差异，训练循环的功能保持不变。利用训练数据，计算模型输出、损失和梯度。然后，使用梯度来更新模型。

Example 4-10. A snippet of the training loop

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# the training routine is these 5 steps:

# --------------------------------------
# step 1. zero the gradients
optimizer.zero_grad()

# step 2. compute the output
y_pred = classifier(batch_dict['x_surname'])

# step 3. compute the loss
loss = loss_func(y_pred, batch_dict['y_nationality'])
loss_batch = loss.to("cpu").item()
running_loss += (loss_batch - running_loss) / (batch_index + 1)

# step 4. use loss to produce gradients
loss.backward()

# step 5. use optimizer to take gradient step
optimizer.step()

Model Evaluation and Prediction

要理解模型的性能，应该使用定量和定性方法分析模型。定量测量出的测试数据的误差，决定了分类器能否推广到不可见的例子。定性地说，可以通过查看分类器的top-k预测来为一个新示例开发模型所了解的内容的直觉。

EVALUATING ON THE TEST DATASET

评价SurnameClassifier测试数据,我们执行相同的常规的routine文本分类的例子“餐馆评论的例子:分类情绪”:我们将数据集设置为遍历测试数据,调用classifier.eval()方法,并遍历测试数据以同样的方式与其他数据。在这个例子中，调用classifier.eval()可以防止PyTorch在使用测试/评估数据时更新模型参数。

该模型对测试数据的准确性达到50%左右。如果在附带的notebook中运行训练例程，会注意到在训练数据上的性能更高。这是因为模型总是更适合它所训练的数据，所以训练数据的性能并不代表新数据的性能。如果遵循代码，你可以尝试隐藏维度的不同大小，应该注意到性能的提高。然而，这种增长不会很大(尤其是与“用CNN对姓氏进行分类的例子”中的模型相比)。其主要原因是收缩的onehot向量化方法是一种弱表示。虽然它确实简洁地将每个姓氏表示为单个向量，但它丢弃了字符之间的顺序信息，这对于识别起源非常重要。

CLASSIFYING A NEW SURNAME

示例4-11显示了分类新姓氏的代码。给定一个姓氏作为字符串，该函数将首先应用向量化过程，然后获得模型预测。注意，我们包含了apply_softmax标志，所以结果包含概率。模型预测，在多项式的情况下，是类概率的列表。我们使用PyTorch张量最大函数来得到由最高预测概率表示的最优类。

Example 4-11. A function for performing nationality prediction

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def predict_nationality(surname, classifier, vectorizer):
    """预测姓氏的国籍
    
    Args:
        surname (str): 要分类的姓氏
        classifier (SurnameClassifer): 分类器的实例
        vectorizer (SurnameVectorizer): 相应的向量化器
    Returns:
        dict: 包含最可能的国籍及其概率的字典
    """
    # 向量化姓氏
    vectorized_surname = vectorizer.vectorize(surname)
    # 将向量化的姓氏转换为PyTorch张量，并添加批次维度
    vectorized_surname = torch.tensor(vectorized_surname).unsqueeze(0)
    # 使用分类器进行预测，并对输出进行softmax处理
    result = classifier(vectorized_surname, apply_softmax=True)

    # 获取概率最高的国籍及其对应的索引
    probability_values, indices = result.max(dim=1)
    index = indices.item()

    # 通过索引查找预测的国籍，并获取其概率值
    predicted_nationality = vectorizer.nationality_vocab.lookup_index(index)
    probability_value = probability_values.item()

    # 返回预测结果的字典
    return {'nationality': predicted_nationality, 'probability': probability_value}

示例：
alt text

RETRIEVING THE TOP-K PREDICTIONS FOR A NEW SURNAME

不仅要看最好的预测，还要看更多的预测。例如，NLP中的标准实践是采用k-best预测并使用另一个模型对它们重新排序。PyTorch提供了一个torch.topk函数，它提供了一种方便的方法来获得这些预测，如示例4-12所示。

Example 4-12. Predicting the top-k nationalities

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def predict_topk_nationality(surname, classifier, vectorizer, k=5):
    """预测姓氏的前K个可能的国籍
    
    Args:
        surname (str): 要分类的姓氏
        classifier (SurnameClassifer): 分类器的实例
        vectorizer (SurnameVectorizer): 相应的向量化器
        k (int): 要返回的前K个国籍数量
    Returns:
        list: 字典的列表，每个字典包含一个国籍和其对应的概率
    """
    # 向量化姓氏
    vectorized_surname = vectorizer.vectorize(surname)
    vectorized_surname = torch.tensor(vectorized_surname).unsqueeze(dim=0)
    # 使用分类器进行预测，并对输出进行softmax处理，获取前K个国籍及其概率
    prediction_vector = classifier(vectorized_surname, apply_softmax=True)
    probability_values, indices = torch.topk(prediction_vector, k=k)
    
    # 获取预测结果中概率最高的K个国籍及其概率值
    probability_values = probability_values[0].detach().numpy()
    indices = indices[0].detach().numpy()
    
    results = []
    for kth_index in range(k):
        # 通过索引查找国籍，并获取其对应的概率值，将结果存储为字典列表
        nationality = vectorizer.nationality_vocab.lookup_index(indices[kth_index])
        probability_value = probability_values[kth_index]
        results.append({'nationality': nationality, 
                        'probability': probability_value})
    return results

示例：
alt text

Regularizing MLPs: Weight Regularization and Structural Regularization (or Dropout)

在实验3中，我们解释了正则化是如何解决过拟合问题的，并研究了两种重要的权重正则化类型——L1和L2。这些权值正则化方法也适用于MLPs和卷积神经网络，我们将在本实验后面介绍。除权值正则化外，对于深度模型(即例如本实验讨论的前馈网络，一种称为dropout的结构正则化方法变得非常重要。

DROPOUT

简单地说，在训练过程中，dropout有一定概率使属于两个相邻层的单元之间的连接减弱。这有什么用呢?我们从斯蒂芬•梅里蒂(Stephen Merity)的一段直观(且幽默)的解释开始：“Dropout，简单地说，是指如果你能在喝醉的时候反复学习如何做一件事，那么你应该能够在清醒的时候做得更好。这一见解产生了许多最先进的结果和一个新兴的领域。”

神经网络——尤其是具有大量分层的深层网络——可以在单元之间创建有趣的相互适应。“Coadaptation”是神经科学中的一个术语，但在这里它只是指一种情况，即两个单元之间的联系变得过于紧密，而牺牲了其他单元之间的联系。这通常会导致模型与数据过拟合。通过概率地丢弃单元之间的连接，我们可以确保没有一个单元总是依赖于另一个单元，从而产生健壮的模型。dropout不会向模型中添加额外的参数，但是需要一个超参数——“drop probability”。drop probability，它是单位之间的连接drop的概率。通常将下降概率设置为0.5。例4-13给出了一个带dropout的MLP的重新实现。

Example 4-13. MLP with dropout

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import torch.nn as nn
import torch.nn.functional as F

class MultilayerPerceptron(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        """
        Args:
            input_dim (int): the size of the input vectors
            hidden_dim (int): the output size of the first Linear layer
            output_dim (int): the output size of the second Linear layer
        """
        super(MultilayerPerceptron, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x_in, apply_softmax=False):
        """The forward pass of the MLP

        Args:
            x_in (torch.Tensor): an input data tensor.
                x_in.shape should be (batch, input_dim)
            apply_softmax (bool): a flag for the softmax activation
                should be false if used with the Cross Entropy losses
        Returns:
            the resulting tensor. tensor.shape should be (batch, output_dim)
        """
        intermediate = F.relu(self.fc1(x_in))
        output = self.fc2(F.dropout(intermediate, p=0.5))

        if apply_softmax:
            output = F.softmax(output, dim=1)
        return output

请注意，dropout只适用于训练期间，不适用于评估期间。作为练习，可以尝试带有dropout的SurnameClassifier模型，看看它如何更改结果。

卷积神经网络

在本实验的第一部分中，我们深入研究了MLPs、由一系列线性层和非线性函数构建的神经网络。mlp不是利用顺序模式的最佳工具。例如，在姓氏数据集中，姓氏可以有(不同长度的)段，这些段可以显示出相当多关于其起源国家的信息(如“O’Neill”中的“O”、“Antonopoulos”中的“opoulos”、“Nagasawa”中的“sawa”或“Zhu”中的“Zh”)。这些段的长度可以是可变的，挑战是在不显式编码的情况下捕获它们。

在本节中，我们将介绍卷积神经网络(CNN)，这是一种非常适合检测空间子结构(并因此创建有意义的空间子结构)的神经网络。CNNs通过使用少量的权重来扫描输入数据张量来实现这一点。通过这种扫描，它们产生表示子结构检测(或不检测)的输出张量。

在本节的其余部分中，我们首先描述CNN的工作方式，以及在设计CNN时应该考虑的问题。我们深入研究CNN超参数，目的是提供直观的行为和这些超参数对输出的影响。最后，我们通过几个简单的例子逐步说明CNNs的机制。在“示例:使用CNN对姓氏进行分类”中，我们将深入研究一个更广泛的示例。

简介

卷积神经网络（英语：convolutional neural network，缩写：CNN）是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。

CNNs的名称和基本功能源于经典的数学运算卷积。卷积已经应用于各种工程学科，包括数字信号处理和计算机图形学。一般来说，卷积使用程序员指定的参数。这些参数被指定来匹配一些功能设计，如突出边缘或抑制高频声音。事实上，许多Photoshop滤镜都是应用于图像的固定卷积运算。然而，在深度学习和本实验中，我们从数据中学习卷积滤波器的参数，因此它对于解决当前的任务是最优的。

卷积神经网络由一个或多个卷积层和顶端的全连通层（对应经典的神经网络）组成，同时也包括关联权重和池化层（pooling layer）。这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比，卷积神经网络在图像和语音识别方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他深度、前馈神经网络，卷积神经网络需要考量的参数更少，使之成为一种颇具吸引力的深度学习结构。

卷积神经网络的灵感来自于动物视觉皮层组织的神经连接方式。单个神经元只对有限区域内的刺激作出反应，不同神经元的感知区域相互重叠从而覆盖整个视野

模型结构

典型的 CNN 由3个部分构成：

1.卷积层

2.池化层

3.全连接层

如果简单来描述的话：

卷积层负责提取图像中的局部特征；池化层用来大幅降低参数量级(降维)；全连接层类似传统神经网络的部分，用来输出想要的结果。

Convolutional layer

卷积层的运算过程如下图，用一个卷积核扫完整张图片：
请使用魔法

这个过程我们可以理解为我们使用一个过滤器（卷积核）来过滤图像的各个小区域，从而得到这些小区域的特征值。

在具体应用中，往往有多个卷积核，可以认为，每个卷积核代表了一种图像模式，如果某个图像块与此卷积核卷积出的值大，则认为此图像块十分接近于此卷积核。如果我们设计了6个卷积核，可以理解：我们认为这个图像上有6种底层纹理模式，也就是我们用6中基础模式就能描绘出一副图像。以下就是25种不同的卷积核的示例：
alt text

Pooling Layer

池化层简单说就是下采样，他可以大大降低数据的维度。其过程如下：
alt text
上图中，我们可以看到，原始图片是20×20的，我们对其进行下采样，采样窗口为10×10，最终将其下采样成为一个2×2大小的特征图。

之所以这么做的原因，是因为即使做完了卷积，图像仍然很大（因为卷积核比较小），所以为了降低数据维度，就进行下采样。

池化层相比卷积层可以更有效的降低数据维度，这么做不但可以大大减少运算量，还可以有效的避免过拟合。

Fully connected layer

这个部分就是最后一步了，经过卷积层和池化层处理过的数据输入到全连接层，得到最终想要的结果。

经过卷积层和池化层降维过的数据，全连接层才能”跑得动”，不然数据量太大，计算成本高，效率低下。
alt text
典型的 CNN 并非只是上面提到的3层结构，而是多层结构，例如 LeNet-5 的结构就如下图所示：

卷积层 – 池化层- 卷积层 – 池化层 – 卷积层 – 全连接层
alt text

DIMENSION OF THE CONVOLUTION OPERATION

首先要理解的概念是卷积运算的维数。在本节，我们使用二维卷积进行说明，但是根据数据的性质，还有更适合的其他维度的卷积。在PyTorch中，卷积可以是一维、二维或三维的，分别由Conv1d、Conv2d和Conv3d模块实现。一维卷积对于每个时间步都有一个特征向量的时间序列非常有用。在这种情况下，我们可以在序列维度上学习模式。NLP中的卷积运算大多是一维的卷积。另一方面，二维卷积试图捕捉数据中沿两个方向的时空模式;例如，在图像中沿高度和宽度维度——为什么二维卷积在图像处理中很流行。类似地，在三维卷积中，模式是沿着数据中的三维捕获的。例如，在视频数据中，信息是三维的，二维表示图像的帧，时间维表示帧的序列。我们主要使用Conv1d。

CHANNELS

非正式地，通道(channel)是指沿输入中的每个点的特征维度。例如，在图像中，对应于RGB组件的图像中的每个像素有三个通道。在使用卷积时，文本数据也可以采用类似的概念。从概念上讲，如果文本文档中的“像素”是单词，那么通道的数量就是词汇表的大小。如果我们更细粒度地考虑字符的卷积，通道的数量就是字符集的大小(在本例中刚好是词汇表)。在PyTorch卷积实现中，输入通道的数量是in_channels参数。卷积操作可以在输出(out_channels)中产生多个通道。您可以将其视为卷积运算符将输入特征维“映射”到输出特征维。下图说明了这个概念。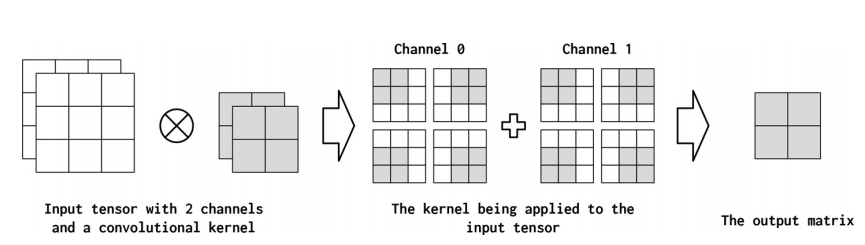

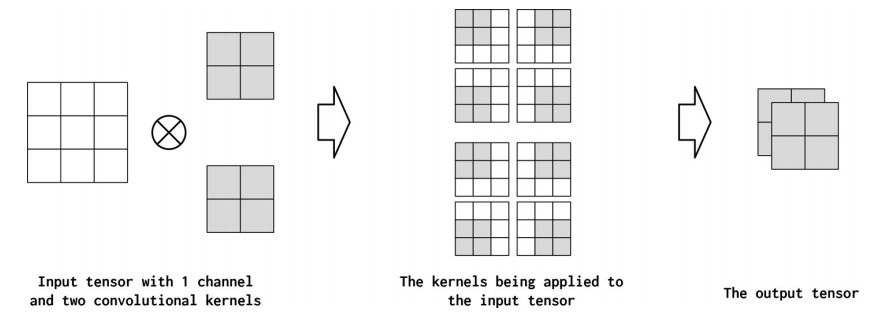
卷积运算用两个输入矩阵（两个输入通道）表示相应的核也有两层，它将每层分别相乘，然后对结果求和。参数配置：input_channels=2, output_channels=1, kernel_size=2, tride=1, padding=0, and dilation=1.


一种具有一个输入矩阵（一个输入通道）和两个卷积的卷积运算核（两个输出通道）。这些核分别应用于输入矩阵，并堆叠在输出张量。参数配置：input_channels=1, output_channels=2, kernel_size=2, tride=1, padding=0, and dilation=1.

很难立即知道有多少输出通道适合当前的问题。为了简化这个困难，我们假设边界是1,1,024——我们可以有一个只有一个通道的卷积层，也可以有一个只有1,024个通道的卷积层。现在我们有了边界，接下来要考虑的是有多少个输入通道。一种常见的设计模式是，从一个卷积层到下一个卷积层，通道数量的缩减不超过2倍。这不是一个硬性的规则，但是它应该让您了解适当数量的out_channels是什么样子的。

KERNEL SIZE

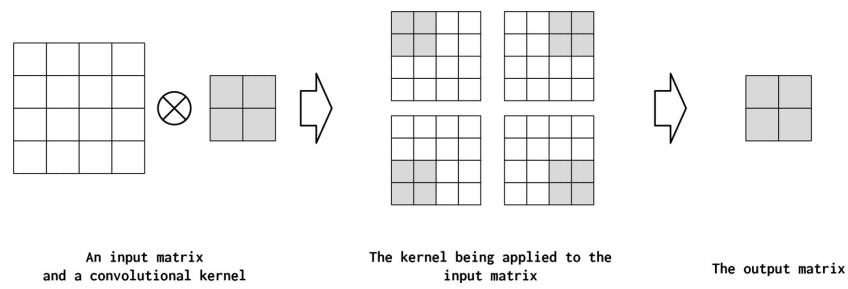
核矩阵的宽度称为核大小(PyTorch中的kernel_size)。我们分别给出一个2x2和3x3的核。卷积将输入中的空间(或时间)本地信息组合在一起，每个卷积的本地信息量由内核大小控制。然而，通过增加核的大小，也会减少输出的大小(Dumoulin和Visin, 2016)。这就是为什么当核大小为3时，输出矩阵2x2，而当核大小为2时，输出矩阵3x3。


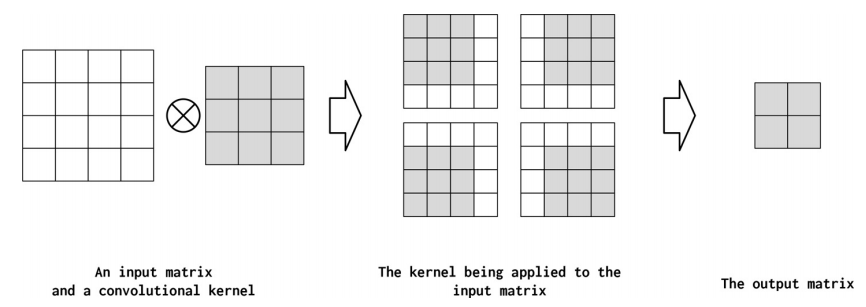
将kernel_size=3的卷积应用于输入矩阵。结果是一个折衷的结果：在每次将内核应用于矩阵时，都会使用更多的局部信息，但输出的大小会更小.

此外，可以将NLP应用程序中核大小的行为看作类似于通过查看单词组捕获语言模式的n-gram的行为。使用较小的核大小，可以捕获较小的频繁模式，而较大的核大小会导致较大的模式，这可能更有意义，但是发生的频率更低。较小的核大小会导致输出中的细粒度特性，而较大的核大小会导致粗粒度特性。

STRIDE

Stride控制卷积之间的步长。如果步长与核相同，则内核计算不会重叠。另一方面，如果跨度为1，则内核重叠最大。输出张量可以通过增加步幅的方式被有意的压缩来总结信息，如下图所示。


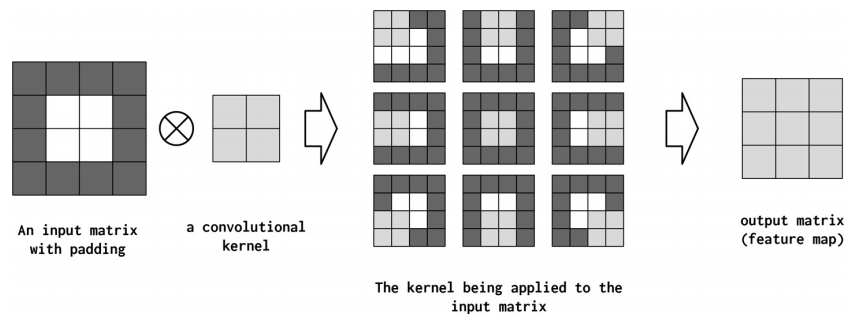
应用于具有超参数步长的输入的kernel_size=2的卷积核等于2。这会导致内核采取更大的步骤，从而产生更小的输出矩阵。对于更稀疏地对输入矩阵进行二次采样非常有用。

PADDING

即使stride和kernel_size允许控制每个计算出的特征值有多大范围，它们也有一个有害的、有时是无意的副作用，那就是缩小特征映射的总大小(卷积的输出)。为了抵消这一点，输入数据张量被人为地增加了长度(如果是一维、二维或三维)、高度(如果是二维或三维)和深度(如果是三维)，方法是在每个维度上附加和前置0。这意味着CNN将执行更多的卷积，但是输出形状可以控制，而不会影响所需的核大小、步幅或扩展。下图展示了正在运行的填充。


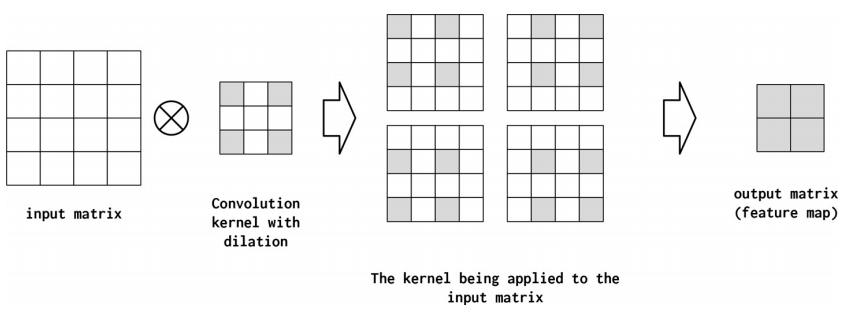
应用于高度和宽度等于的输入矩阵的kernel_size=2的卷积2。但是，由于填充（用深灰色正方形表示），输入矩阵的高度和宽度可以被放大。这通常与大小为3的内核一起使用，这样输出矩阵将等于输入矩阵的大小。

DILATION

膨胀控制卷积核如何应用于输入矩阵。在下图中，我们显示，将膨胀从1(默认值)增加到2意味着当应用于输入矩阵时，核的元素彼此之间是两个空格。另一种考虑这个问题的方法是在核中跨跃——在核中的元素或核的应用之间存在一个step size，即存在“holes”。这对于在不增加参数数量的情况下总结输入空间的更大区域是有用的。当卷积层被叠加时，扩张卷积被证明是非常有用的。连续扩张的卷积指数级地增大了“接受域”的大小；即网络在做出预测之前所看到的输入空间的大小。


应用于超参数dilation=2的输入矩阵的kernel_size=2的卷积。从默认值开始膨胀的增加意味着核矩阵的元素在与输入矩阵相乘时进一步分散开来。进一步增大扩张会加剧这种扩散。

基于卷积神经网络的姓氏分类

Implementing CNNs in PyTorch

在本节中，我们将通过端到端示例来利用上一节中介绍的概念。一般来说，神经网络设计的目标是找到一个能够完成任务的超参数组态。我们再次考虑在“示例:带有多层感知器的姓氏分类”中引入的现在很熟悉的姓氏分类任务，但是我们将使用CNNs而不是MLP。我们仍然需要应用最后一个线性层，它将学会从一系列卷积层创建的特征向量创建预测向量。这意味着目标是确定卷积层的配置，从而得到所需的特征向量。所有CNN应用程序都是这样的:首先有一组卷积层，它们提取一个feature map，然后将其作为上游处理的输入。在分类中，上游处理几乎总是应用线性(或fc)层。

本课程中的实现遍历设计决策，以构建一个特征向量。我们首先构造一个人工数据张量，以反映实际数据的形状。数据张量的大小是三维的——这是向量化文本数据的最小批大小。如果你对一个字符序列中的每个字符使用onehot向量，那么onehot向量序列就是一个矩阵，而onehot矩阵的小批量就是一个三维张量。使用卷积的术语，每个onehot(通常是词汇表的大小)的大小是”input channels”的数量，字符序列的长度是“width”。

在例4-14中，构造特征向量的第一步是将PyTorch的Conv1d类的一个实例应用到三维数据张量。通过检查输出的大小，你可以知道张量减少了多少。

Example 4-14. Artificial data and using a Conv1d class

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class SurnameDataset(Dataset):
    def __getitem__(self, index):
        """PyTorch数据集的主要入口方法
        
        参数:
            index (int): 数据点的索引 
        返回:
            一个字典，保存数据点的特征（x_data）和标签（y_target）
        """
        row = self._target_df.iloc[index]

        surname_matrix = \
            self._vectorizer.vectorize(row.surname)

        nationality_index = \
            self._vectorizer.nationality_vocab.lookup_token(row.nationality)

        return {'x_surname': surname_matrix,
                'y_nationality': nationality_index}

Vocabulary, Vectorizer, and DataLoader

在本例中，尽管词汇表和DataLoader的实现方式与“示例:带有多层感知器的姓氏分类”中的示例相同，但Vectorizer的vectorize()方法已经更改，以适应CNN模型的需要。具体来说，正如我们在示例4-18中的代码中所示，该函数将字符串中的每个字符映射到一个整数，然后使用该整数构造一个由onehot向量组成的矩阵。重要的是，矩阵中的每一列都是不同的onehot向量。主要原因是，我们将使用的Conv1d层要求数据张量在第0维上具有批处理，在第1维上具有通道，在第2维上具有特性。

除了更改为使用onehot矩阵之外，我们还修改了矢量化器，以便计算姓氏的最大长度并将其保存为max_surname_length

Example 4-18. Implementing the Surname Vectorizer for CNNs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class SurnameVectorizer(object):
    """协调词汇表并将它们应用到使用的向量化器"""
    def __init__(self, surname_vocab, nationality_vocab, max_surname_length):
        """
        参数:
            surname_vocab (Vocabulary): 将字符映射到整数的词汇表
            nationality_vocab (Vocabulary): 将国籍映射到整数的词汇表
            max_surname_length (int): 最长姓氏的长度
        """
        self.surname_vocab = surname_vocab
        self.nationality_vocab = nationality_vocab
        self._max_surname_length = max_surname_length

    def vectorize(self, surname):
        """
        参数:
            surname (str): 姓氏
        返回:
            one_hot_matrix (np.ndarray): 一个one-hot向量的矩阵
        """

        one_hot_matrix_size = (len(self.surname_vocab), self._max_surname_length)
        one_hot_matrix = np.zeros(one_hot_matrix_size, dtype=np.float32)
                               
        for position_index, character in enumerate(surname):
            character_index = self.surname_vocab.lookup_token(character)
            one_hot_matrix[character_index][position_index] = 1
        
        return one_hot_matrix

Reimplementing the SurnameClassifier with Convolutional Networks

我们在本例中使用的模型是使用我们在“卷积神经网络”中介绍的方法构建的。实际上，我们在该部分中创建的用于测试卷积层的“人工”数据与姓氏数据集中使用本例中的矢量化器的数据张量的大小完全匹配。正如在示例4-19中所看到的，它与我们在“卷积神经网络”中引入的Conv1d序列既有相似之处，也有需要解释的新添加内容。具体来说，该模型类似于“卷积神经网络”，它使用一系列一维卷积来增量地计算更多的特征，从而得到一个单特征向量。

然而，本例中的新内容是使用sequence和ELU PyTorch模块。序列模块是封装线性操作序列的方便包装器。在这种情况下，我们使用它来封装Conv1d序列的应用程序。ELU是类似于实验3中介绍的ReLU的非线性函数，但是它不是将值裁剪到0以下，而是对它们求幂。ELU已经被证明是卷积层之间使用的一种很有前途的非线性(Clevert et al.， 2015)。

在本例中，我们将每个卷积的通道数与num_channels超参数绑定。我们可以选择不同数量的通道分别进行卷积运算。这样做需要优化更多的超参数。我们发现256足够大，可以使模型达到合理的性能。

Example 4-19. The CNN-based SurnameClassifier

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import torch.nn as nn
import torch.nn.functional as F

class SurnameClassifier(nn.Module):
    def __init__(self, initial_num_channels, num_classes, num_channels):
        """
        创建一个姓氏分类器。
        
        参数:
            initial_num_channels (int): 输入特征向量的大小
            num_classes (int): 输出预测向量的大小
            num_channels (int): 网络中要始终使用的恒定通道大小
        """
        super(SurnameClassifier, self).__init__()
        
        self.convnet = nn.Sequential(
            nn.Conv1d(in_channels=initial_num_channels, 
                      out_channels=num_channels, kernel_size=3),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels, 
                      kernel_size=3, stride=2),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels, 
                      kernel_size=3, stride=2),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels, 
                      kernel_size=3),
            nn.ELU()
        )
        self.fc = nn.Linear(num_channels, num_classes)

    def forward(self, x_surname, apply_softmax=False):
        """分类器的前向传播
        
        参数:
            x_surname (torch.Tensor): 输入数据张量。
                x_surname.shape 应为 (batch, initial_num_channels, max_surname_length)
            apply_softmax (bool): softmax 激活的标志
                如果与交叉熵损失一起使用，则应为 False
        返回:
            结果张量。tensor.shape 应为 (batch, num_classes)
        """
        features = self.convnet(x_surname).squeeze(dim=2)
       
        prediction_vector = self.fc(features)

        if apply_softmax:
            prediction_vector = F.softmax(prediction_vector, dim=1)

        return prediction_vector

The Training Routine

训练程序包括以下似曾相识的的操作序列:实例化数据集,实例化模型,实例化损失函数,实例化优化器,遍历数据集的训练分区和更新模型参数,遍历数据集的验证分区和测量性能,然后重复数据集迭代一定次数。此时，这是本书到目前为止的第三个训练例程实现，应该将这个操作序列内部化。对于这个例子，我们将不再详细描述具体的训练例程，因为它与“示例:带有多层感知器的姓氏分类”中的例程完全相同。但是，输入参数是不同的，可以在示例4-20中看到。

Example 4-20. Input arguments to the CNN surname classifier

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
args = Namespace(
    # 数据和路径信息
    surname_csv="data/surnames/surnames_with_splits.csv",
    vectorizer_file="vectorizer.json",
    model_state_file="model.pth",
    save_dir="model_storage/ch4/cnn",
    # 模型超参数
    hidden_dim=100,
    num_channels=256,
    # 训练超参数
    seed=1337,
    learning_rate=0.001,
    batch_size=128,
    num_epochs=100,
    early_stopping_criteria=5,
    dropout_p=0.1,
    # 运行时选项
    cuda=False,
    reload_from_files=False,
    expand_filepaths_to_save_dir=True,
    catch_keyboard_interrupt=True
)

Model Evaluation and Prediction

要理解模型的性能，需要对性能进行定量和定性的度量。下面将描述这两个度量的基本组件。

Evaluating on the Test Dataset

正如“示例:带有多层感知器的姓氏分类”中的示例与本示例之间的训练例程没有变化一样，执行评估的代码也没有变化。总之，调用分类器的eval()方法来防止反向传播，并迭代测试数据集。与 MLP 约 50% 的性能相比，该模型的测试集性能准确率约为56%。尽管这些性能数字绝不是这些特定架构的上限，但是通过一个相对简单的CNN模型获得的改进应该足以让您在文本数据上尝试CNNs。

Classifying or retrieving top predictions for a new surname

在本例中，predict_nationality()函数的一部分发生了更改，如例4-21:我们没有使用视图方法重塑新创建的数据张量以添加批处理维度，而是使用PyTorch的unsqueeze()函数在批处理应该在的位置添加大小为1的维度。相同的更改反映在predict_topk_nationality()函数中。

Example 4-21. Using the trained model to make predictions

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def predict_nationality(surname, classifier, vectorizer):
    """预测姓氏的国籍
    
    Args:
        surname (str): 要分类的姓氏
        classifier (SurnameClassifer): 分类器的实例
        vectorizer (SurnameVectorizer): 相应的向量化器
    Returns:
        dict: 包含最可能的国籍及其概率的字典
    """
    # 向量化姓氏
    vectorized_surname = vectorizer.vectorize(surname)
    # 将向量化的姓氏转换为PyTorch张量，并添加批次维度
    vectorized_surname = torch.tensor(vectorized_surname).unsqueeze(0)
    # 使用分类器进行预测，并对输出进行softmax处理
    result = classifier(vectorized_surname, apply_softmax=True)

    # 获取概率最高的国籍及其对应的索引
    probability_values, indices = result.max(dim=1)
    index = indices.item()

    # 通过索引查找预测的国籍，并获取其概率值
    predicted_nationality = vectorizer.nationality_vocab.lookup_index(index)
    probability_value = probability_values.item()

    # 返回预测结果的字典
    return {'nationality': predicted_nationality, 'probability': probability_value}

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def predict_topk_nationality(surname, classifier, vectorizer, k=5):
    """预测姓氏的前K个可能的国籍
    
    Args:
        surname (str): 要分类的姓氏
        classifier (SurnameClassifer): 分类器的实例
        vectorizer (SurnameVectorizer): 相应的向量化器
        k (int): 要返回的前K个国籍数量
    Returns:
        list: 字典的列表，每个字典包含一个国籍和其对应的概率
    """
    # 向量化姓氏
    vectorized_surname = vectorizer.vectorize(surname)
    vectorized_surname = torch.tensor(vectorized_surname).unsqueeze(dim=0)
    # 使用分类器进行预测，并对输出进行softmax处理，获取前K个国籍及其概率
    prediction_vector = classifier(vectorized_surname, apply_softmax=True)
    probability_values, indices = torch.topk(prediction_vector, k=k)
    
    # 获取预测结果中概率最高的K个国籍及其概率值
    probability_values = probability_values[0].detach().numpy()
    indices = indices[0].detach().numpy()
    
    results = []
    for kth_index in range(k):
        # 通过索引查找国籍，并获取其对应的概率值，将结果存储为字典列表
        nationality = vectorizer.nationality_vocab.lookup_index(indices[kth_index])
        probability_value = probability_values[kth_index]
        results.append({'nationality': nationality, 
                        'probability': probability_value})
    return results

new_surname = input("Enter a surname to classify: ")

k = int(input("How many of the top predictions to see? "))
if k > len(vectorizer.nationality_vocab):
    print("Sorry! That's more than the # of nationalities we have.. defaulting you to max size :)")
    k = len(vectorizer.nationality_vocab)
    
# 调用函数进行预测并打印结果
predictions = predict_topk_nationality(new_surname, classifier, vectorizer, k=k)

print("Top {} predictions:".format(k))
print("===================")
for prediction in predictions:
    print("{} -> {} (p={:0.2f})".format(new_surname,
                                        prediction['nationality'],
                                        prediction['probability']))

示例：

Miscellaneous Topics in CNNs

为了结束我们的讨论，我们概述了几个其他的主题，这些主题是CNNs的核心，但在它们的共同使用中起着主要作用。特别是，你将看到Pooling操作、batch Normalization、network-in-network connection和residual connections的描述。

Pooling Operation

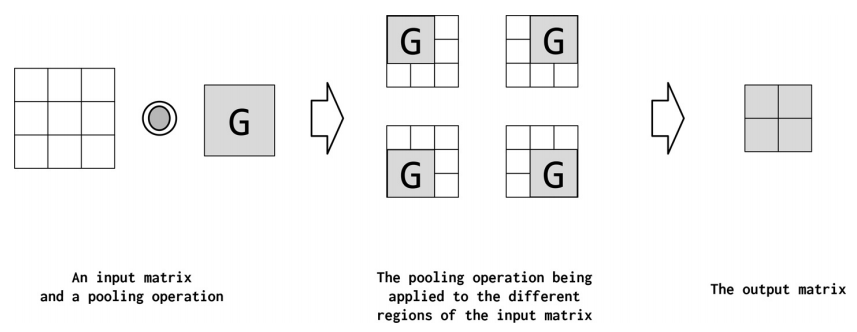
Pooling是将高维特征映射总结为低维特征映射的操作。卷积的输出是一个特征映射。feature map中的值总结了输入的一些区域。由于卷积计算的重叠性，许多计算出的特征可能是冗余的。Pooling是一种将高维(可能是冗余的)特征映射总结为低维特征映射的方法。在形式上，池是一种像sum、mean或max这样的算术运算符，系统地应用于feature map中的局部区域，得到的池操作分别称为sum pooling、average pooling和max pooling。池还可以作为一种方法，将较大但较弱的feature map的统计强度改进为较小但较强的feature map。下图说明了Pooling。


这里所示的池操作在功能上与卷积相同：它应用于输入矩阵中的不同位置。然而，池操作不是将输入矩阵的值相乘和求和，而是应用一些函数G来汇集这些值。G可以是任何运算，但求和、求最大值和计算平均值是最常见的。

Batch Normalization (BatchNorm)

批处理标准化是设计网络时经常使用的一种工具。BatchNorm对CNN的输出进行转换，方法是将激活量缩放为零均值和单位方差。它用于Z-transform的平均值和方差值每批更新一次，这样任何单个批中的波动都不会太大地移动或影响它。BatchNorm允许模型对参数的初始化不那么敏感，并且简化了学习速率的调整(Ioffe and Szegedy, 2015)。在PyTorch中，批处理规范是在nn模块中定义的。例4-22展示了如何用卷积和线性层实例化和使用批处理规范。

Example 4-22. Using s Conv1D layer with batch normalization.

1
2
3
4
5
6
7
8
9
10
    self.conv1 = nn.Conv1d(in_channels=1, out_channels=10,
                           kernel_size=5,
                           stride=1)
    self.conv1_bn = nn.BatchNorm1d(num_features=10)
    # ...

def forward(self, x):
   # ...
   x = F.relu(self.conv1(x))
   x = self.conv1_bn(x)

Network-in-Network Connections (1x1 Convolutions)

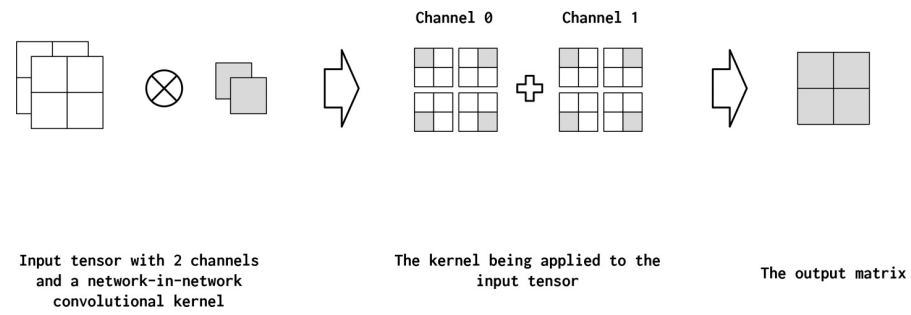
Network-in-Network (NiN)连接是具有kernel_size=1的卷积内核，具有一些有趣的特性。具体来说，1x1卷积就像通道之间的一个完全连通的线性层。这在从多通道feature map映射到更浅的feature map时非常有用。在下图中，我们展示了一个应用于输入矩阵的NiN连接。它将两个通道简化为一个通道。因此，NiN或1x1卷积提供了一种廉价的方法来合并参数较少的额外非线性(Lin et al.， 2013)。


一个1×1卷积运算的例子。观察1×1卷积是如何进行的操作将通道数从两个减少到一个。

Residual Connections/Residual Block

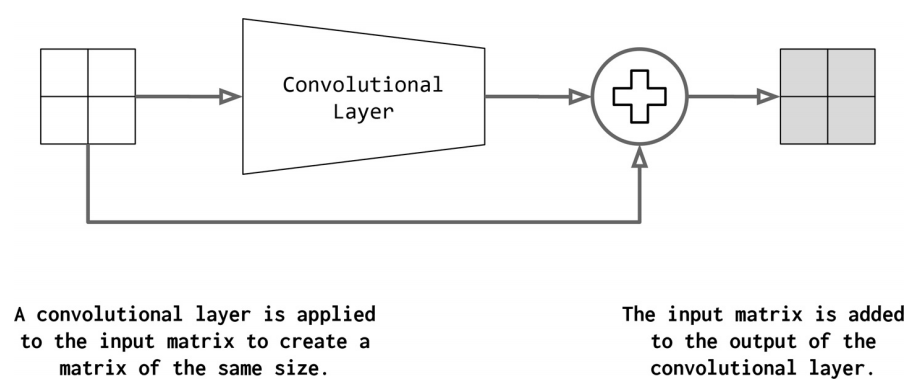
CNNs中最重要的趋势之一是Residual connection，它支持真正深层的网络(超过100层)。它也称为skip connection。如果将卷积函数表示为conv，则residual block的输出如下:

$$output = conv ( input ) + input$$

然而，这个操作有一个隐含的技巧，如图下所示。对于要添加到卷积输出的输入，它们必须具有相同的形状。为此，标准做法是在卷积之前应用填充。在图4-15中，填充尺寸为1，卷积大小为3。


残差连接是一种将原始矩阵加到卷积输出上的方法。当将卷积层应用于输入矩阵并将结果添加到输入矩阵时，以上直观地描述了这一点。创建与输入大小相同的输出的通用超参数设置是让kernel_size=3和padding=1。一般来说，任何带 adding=(floor(kernel_size)/2-1) 的奇数内核大小都将导致与输入大小相同的输出。卷积层产生的矩阵被加到输入端，最后的结果是剩余连接计算的输出端。