背景知识

注意力机制

本篇章将从attention开始，逐步对Transformer结构所涉及的知识进行深入讲解，希望能给读者以形象生动的描述。

问题：Attention出现的原因是什么？
潜在的答案：基于循环神经网络（RNN）一类的seq2seq模型，在处理长文本时遇到了挑战，而对长文本中不同位置的信息进行attention有助于提升RNN的模型效果。

于是学习的问题就拆解为：1. 什么是seq2seq模型？2. 基于RNN的seq2seq模型如何处理文本/长文本序列？3. seq2seq模型处理长文本序列时遇到了什么问题？4.基于RNN的seq2seq模型如何结合attention来改善模型效果？

seq2seq框架

seq2seq是一种常见的NLP模型结构，全称是：sequence to sequence，翻译为“序列到序列”。顾名思义：从一个文本序列得到一个新的文本序列。典型的任务有：机器翻译任务，文本摘要任务。谷歌翻译在2016年末开始使用seq2seq模型，并发表了2篇开创性的论文：Sutskever等2014年发表的Sequence to Sequence Learning with Neural Networks和Cho等2014年发表的Learning Phrase Representations using RNN Encoder–Decoder
for Statistical Machine Translation，感兴趣的读者可以阅读原文进行学习。

无论读者是否读过上述两篇谷歌的文章，NLP初学者想要充分理解并实现seq2seq模型很不容易。因为，我们需要拆解一系列相关的NLP概念，而这些NLP概念又是是层层递进的，所以想要清晰的对seq2seq模型有一个清晰的认识并不容易。但是，如果能够把这些复杂生涩的NLP概念可视化，理解起来其实就更简单了。因此，本文希望通过一系列图片、动态图帮助NLP初学者学习seq2seq以及attention相关的概念和知识。

首先看seq2seq干了什么事情？seq2seq模型的输入可以是一个（单词、字母或者图像特征）序列，输出是另外一个（单词、字母或者图像特征）序列。一个训练好的seq2seq模型如下图所示（注释：将鼠标放在图上，图就会动起来）：

动态图：seq2seq

如下图所示，以NLP中的机器翻译任务为例，序列指的是一连串的单词，输出也是一连串单词。
动态图：translation

seq2seq细节

将上图中蓝色的seq2seq模型进行拆解，如下图所示：seq2seq模型由编码器（Encoder）和解码器（Decoder）组成。绿色的编码器会处理输入序列中的每个元素并获得输入信息，这些信息会被转换成为一个黄色的向量（称为context向量）。当我们处理完整个输入序列后，编码器把 context向量发送给紫色的解码器，解码器通过context向量中的信息，逐个元素输出新的序列。

动态图：seq2seq中的encoder-decoder

由于seq2seq模型可以用来解决机器翻译任务，因此机器翻译被任务seq2seq模型解决过程如下图所示，当作seq2seq模型的一个具体例子来学习。

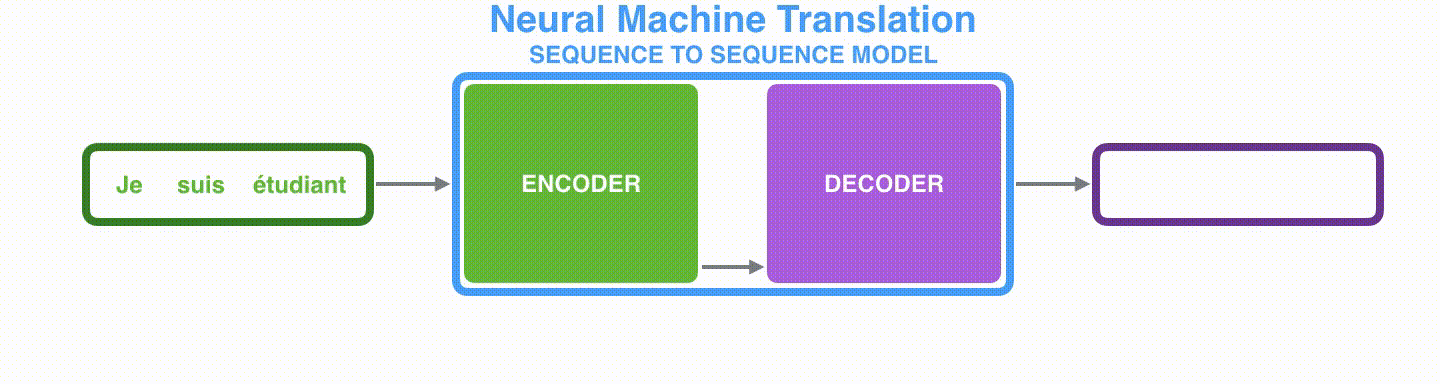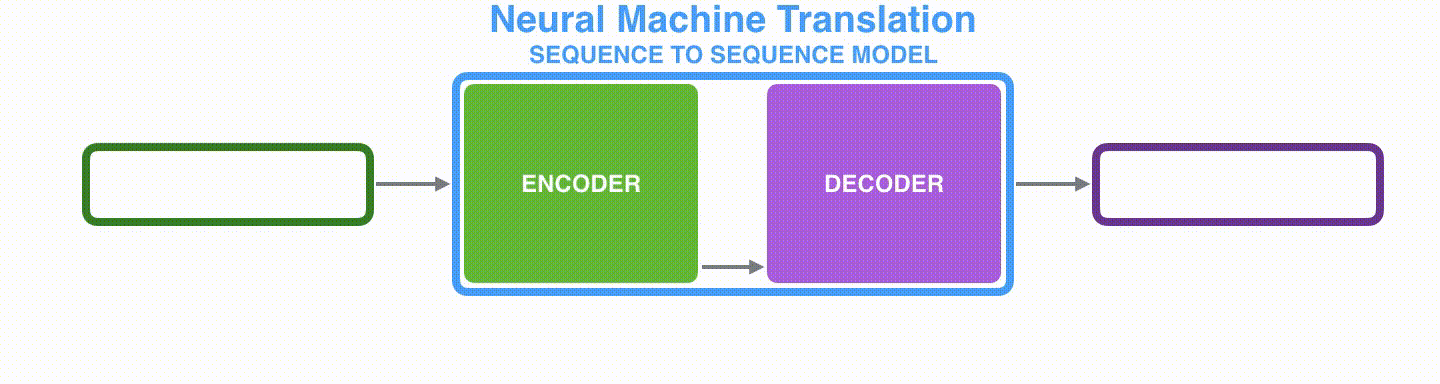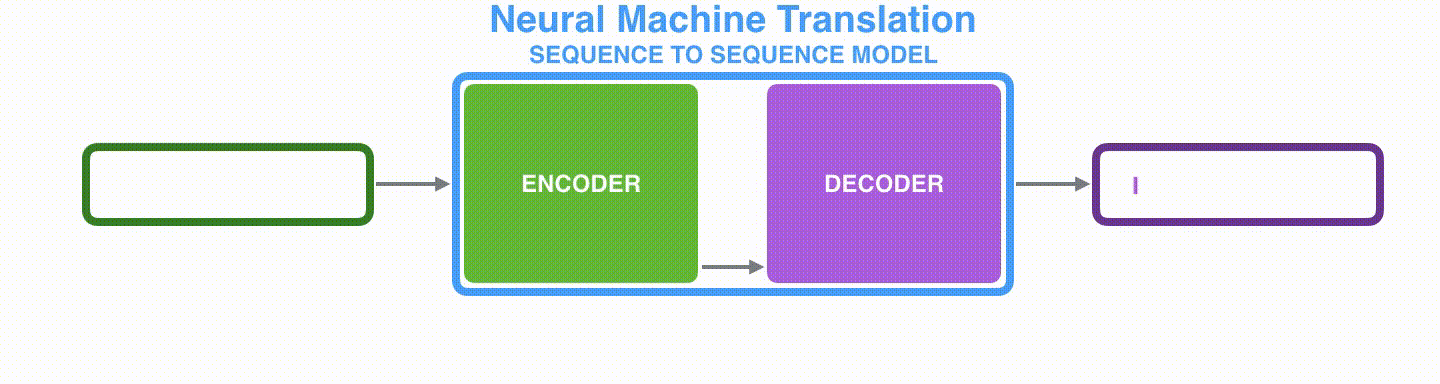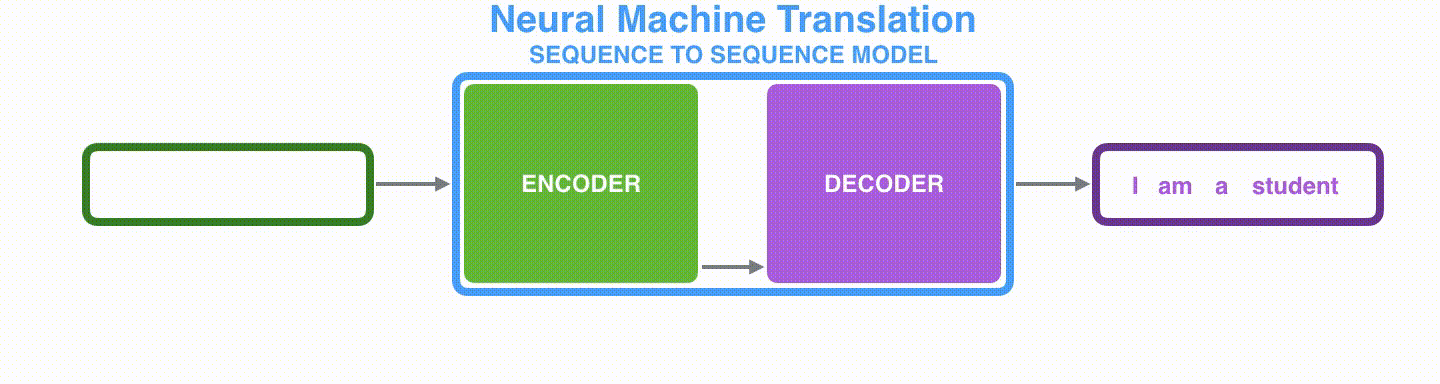动态图：seq2seq中的encoder-decoder，机器翻译的例子

深入学习机器翻译任务中的seq2seq模型，如下图所示。seq2seq模型中的编码器和解码器一般采用的是循环神经网络RNN（Transformer模型还没出现的过去时代）。编码器将输入的法语单词序列编码成context向量（在绿色encoder和紫色decoder中间出现），然后解码器根据context向量解码出英语单词序列。*

图：context向量对应上图中间浮点数向量。在下文中，我们会可视化这些数字向量，使用更明亮的色彩来表示更高的值，如上图右边所示

如上图所示，我们来看一下黄色的context向量是什么？本质上是一组浮点数。而这个context的数组长度是基于编码器RNN的隐藏层神经元数量的。上图展示了长度为4的context向量，但在实际应用中，context向量的长度是自定义的，比如可能是256，512或者1024。

那么RNN是如何具体地处理输入序列的呢？

假设序列输入是一个句子，这个句子可以由$n$个词表示：$sentence = {w_1, w_2,…,w_n}$。
RNN首先将句子中的每一个词映射成为一个向量得到一个向量序列：$X = {x_1, x_2,…,x_n}$，每个单词映射得到的向量通常又叫做：word embedding。
然后在处理第$t \in [1,n]$个时间步的序列输入$x_t$时，RNN网络的输入和输出可以表示为：$h_{t} = RNN(x_t, h_{t-1})$
- 输入：RNN在时间步$t$的输入之一为单词$w_t$经过映射得到的向量$x_t$。
- 输入：RNN另一个输入为上一个时间步$t-1$得到的hidden state向量$h_{t-1}$，同样是一个向量。
- 输出：RNN在时间步$t$的输出为$h_t$ hidden state向量。

图：word embedding例子。我们在处理单词之前，需要将单词映射成为向量，通常使用 word embedding 算法来完成。一般来说，我们可以使用提前训练好的 word embeddings，或者在自有的数据集上训练word embedding。为了简单起见，上图展示的word embedding维度是4。上图左边每个单词经过word embedding算法之后得到中间一个对应的4维的向量。

让我们来进一步可视化一下基于RNN的seq2seq模型中的编码器在第1个时间步是如何工作：

动态图：如图所示，RNN在第2个时间步，采用第1个时间步得到hidden state#10（隐藏层状态）和第2个时间步的输入向量input#1，来得到新的输出hidden state#1。

看下面的动态图，让我们详细观察一下编码器如何在每个时间步得到hidden sate，并将最终的hidden state传输给解码器，解码器根据编码器所给予的最后一个hidden state信息解码处输出序列。注意，最后一个 hidden state实际上是我们上文提到的context向量。
动态图：编码器逐步得到hidden state并传输最后一个hidden state给解码器。

接着，结合编码器处理输入序列，一起来看下解码器如何一步步得到输出序列的l。与编码器类似，解码器在每个时间步也会得到 hidden state（隐藏层状态），而且也需要把 hidden state（隐藏层状态）从一个时间步传递到下一个时间步。

动态图：编码器首先按照时间步依次编码每个法语单词，最终将最后一个hidden state也就是context向量传递给解码器，解码器根据context向量逐步解码得到英文输出。

目前为止，希望你已经明白了本文开头提出的前两个问题：1. 什么是seq2seq模型？2. seq2seq模型如何处理文本/长文本序列？那么请思考第3、4个问题：3. seq2seq模型处理文本序列（特别是长文本序列）时会遇到什么问题？4.基于RNN的seq2seq模型如何结合attention来解决问题3并提升模型效果？

Attention

基于RNN的seq2seq模型编码器所有信息都编码到了一个context向量中，便是这类模型的瓶颈。一方面单个向量很难包含所有文本序列的信息，另一方面RNN递归地编码文本序列使得模型在处理长文本时面临非常大的挑战（比如RNN处理到第500个单词的时候，很难再包含1-499个单词中的所有信息了）。

面对以上问题，Bahdanau等2014发布的Neural Machine Translation by Jointly Learning to Align and Translate 和 Luong等2015年发布的Effective Approaches to Attention-based Neural Machine Translation 两篇论文中，提出了一种叫做注意力attetion的技术。通过attention技术，seq2seq模型极大地提高了机器翻译的质量。归其原因是：attention注意力机制，使得seq2seq模型可以有区分度、有重点地关注输入序列。

下图依旧是机器翻译的例子：

图：在第 7 个时间步，注意力机制使得解码器在产生英语翻译student英文翻译之前，可以将注意力集中在法语输入序列的：étudiant。这种有区分度得attention到输入序列的重要信息，使得模型有更好的效果。

让我们继续来理解带有注意力的seq2seq模型：一个注意力模型与经典的seq2seq模型主要有2点不同：

A. 首先，编码器会把更多的数据传递给解码器。编码器把所有时间步的 hidden state（隐藏层状态）传递给解码器，而不是只传递最后一个 hidden state（隐藏层状态），如下面的动态图所示:
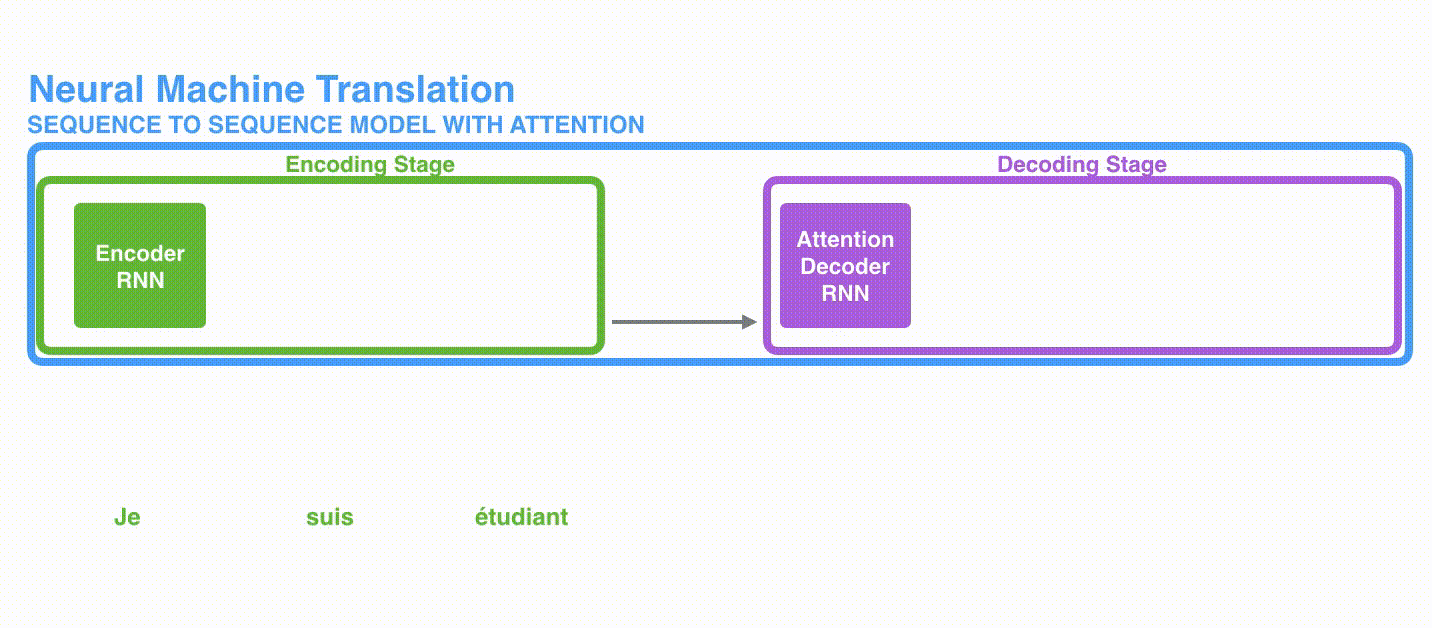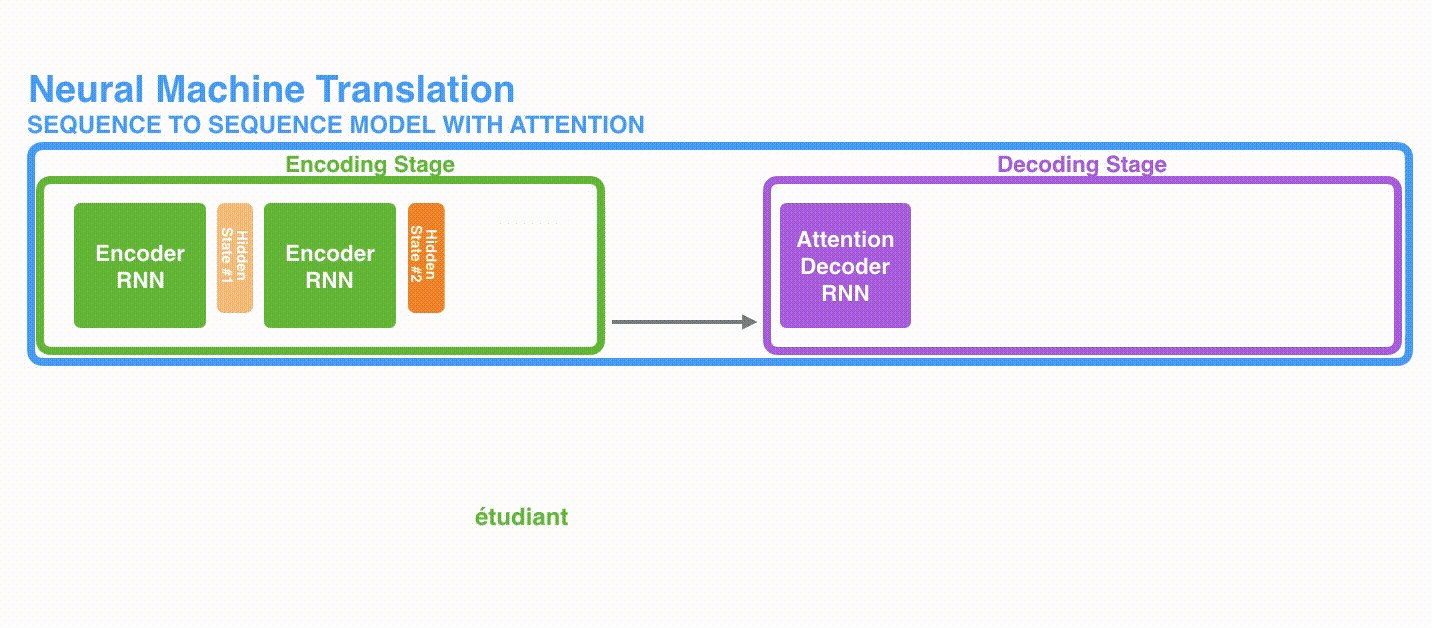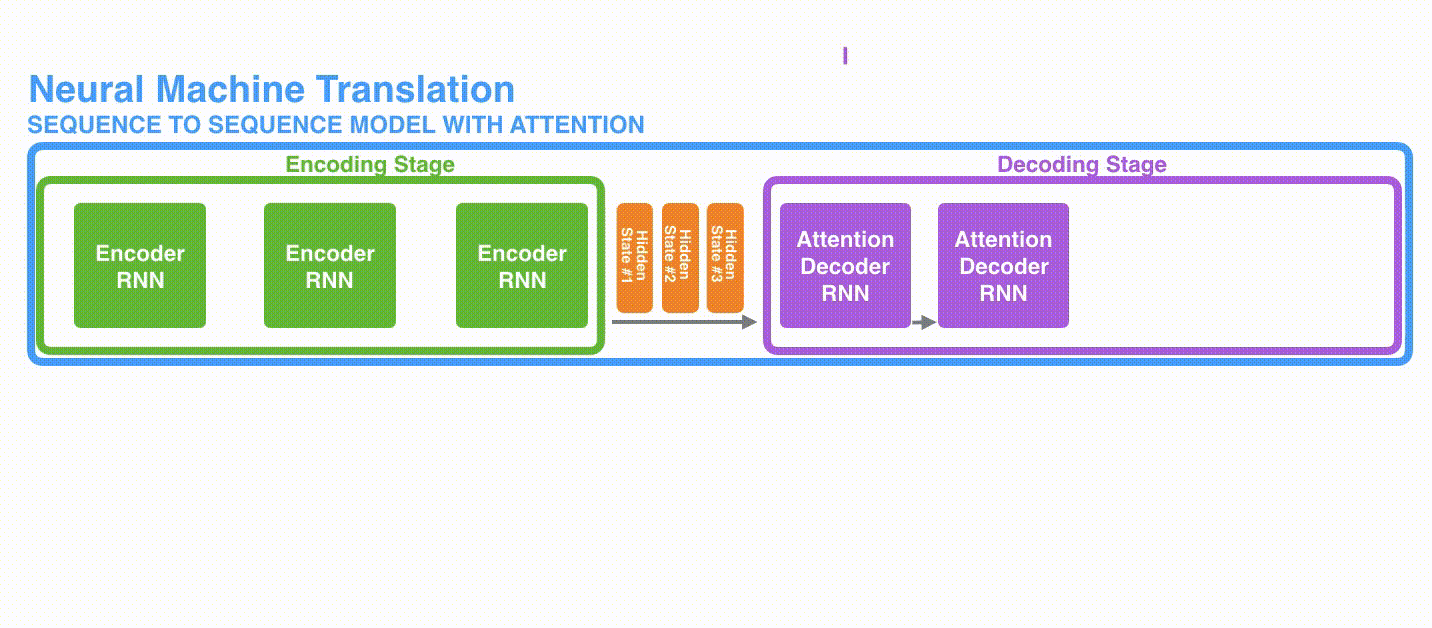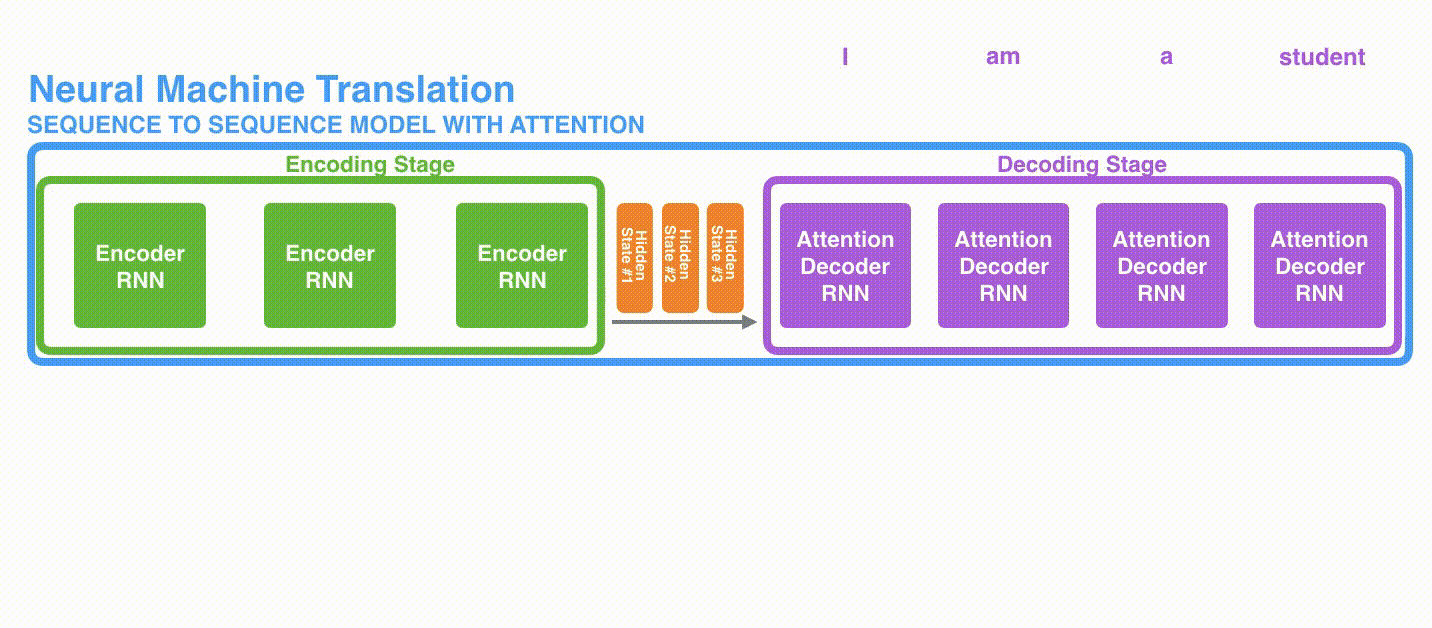动态图: 更多的信息传递给decoder
B. 注意力模型的解码器在产生输出之前，做了一个额外的attention处理。如下图所示，具体为：
- 1. 由于编码器中每个 hidden state（隐藏层状态）都对应到输入句子中一个单词，那么解码器要查看所有接收到的编码器的 hidden state（隐藏层状态）。
- 1. 给每个 hidden state（隐藏层状态）计算出一个分数（我们先忽略这个分数的计算过程）。
- 1. 所有hidden state（隐藏层状态）的分数经过softmax进行归一化。
- 1. 将每个 hidden state（隐藏层状态）乘以所对应的分数，从而能够让高分对应的 hidden state（隐藏层状态）会被放大，而低分对应的 hidden state（隐藏层状态）会被缩小。
- 1. 将所有hidden state根据对应分数进行加权求和，得到对应时间步的context向量。
    动态图：在第4个时间步，编码器结合attention得到context向量的5个步骤。

所以，attention可以简单理解为：一种有效的加权求和技术，其艺术在于如何获得权重。

现在，让我们把所有内容都融合到下面的图中，来看看结合注意力的seq2seq模型解码器全流程，动态图展示的是第4个时间步：

注意力模型的解码器 RNN 的输入包括：一个word embedding 向量，和一个初始化好的解码器 hidden state，图中是$h_{init}$。
RNN 处理上述的 2 个输入，产生一个输出和一个新的 hidden state，图中为h4。
注意力的步骤：我们使用编码器的所有 hidden state向量和 h4 向量来计算这个时间步的context向量（C4）。
我们把 h4 和 C4 拼接起来，得到一个橙色向量。
我们把这个橙色向量输入一个前馈神经网络（这个网络是和整个模型一起训练的）。
根据前馈神经网络的输出向量得到输出单词：假设输出序列可能的单词有N个，那么这个前馈神经网络的输出向量通常是N维的，每个维度的下标对应一个输出单词，每个维度的数值对应的是该单词的输出概率。
在下一个时间步重复1-6步骤。
动态图：解码器结合attention全过程

到目前为止，希望你已经知道本文开头提出的3、4问题的答案啦：3、seq2seq处理长文本序列的挑战是什么？4、seq2seq是如何结合attention来解决问题3中的挑战的？

最后，我们可视化一下注意力机制，看看在解码器在每个时间步关注了输入序列的哪些部分：
动态图：解码步骤时候attention关注的词

需要注意的是：注意力模型不是无意识地把输出的第一个单词对应到输入的第一个单词，它是在训练阶段学习到如何对两种语言的单词进行对应（在我们的例子中，是法语和英语）。

下图还展示了注意力机制的准确程度（图片来自于上面提到的论文）：
图：可以看到模型在输出 “European Economic Area” 时，注意力分布情况。在法语中，这些单词的顺序，相对于英语，是颠倒的（”européenne économique zone”）。而其他词的顺序是类似的。

transformer

我们知晓了attention为循环神经网络带来的优点。那么有没有一种神经网络结构直接基于attention构造，并且不再依赖RNN、LSTM或者CNN网络结构了呢？答案便是：Transformer。因此，我们将在本小节对Transformer所涉及的细节进行深入探讨。

Transformer模型在2017年被google提出，直接基于Self-Attention结构，取代了之前NLP任务中常用的RNN神经网络结构，并在WMT2014 Englishto-German和WMT2014 English-to-French两个机器翻译任务上都取得了当时的SOTA。

与RNN这类神经网络结构相比，Transformer一个巨大的优点是：模型在处理序列输入时，可以对整个序列输入进行并行计算，不需要按照时间步循环递归处理输入序列。。

下图先便是Transformer整体结构图，与seq2seq模型类似，Transformer模型结构中的左半部分为编码器（encoder），右半部分为解码器（decoder），下面我们来一步步拆解 Transformer。

图：transformer模型结构

Transformer宏观结构

Transformer最开始提出来解决机器翻译任务，因此可以看作是seq2seq模型的一种。本小节先抛开Transformer模型中结构具体细节，先从seq2seq的角度对Transformer进行宏观结构的学习。以机器翻译任务为例，先将Transformer这种特殊的seqseq模型看作一个黑盒，黑盒的输入是法语文本序列，输出是英语文本序列（对比seq2seq框架知识我们可以发现，Transformer宏观结构属于seq2seq范畴，只是将之前seq2seq中的编码器和解码器，从RNN模型替换成了Transformer模型）。

图：Transformer黑盒输入和输出

将上图中的中间部分“THE TRANSFORMER”拆开成seq2seq标准结构，得到下图：左边是编码部分encoders，右边是解码器部分decoders。

图：encoder-decoder

下面，再将上图中的编码器和解码器细节绘出，得到下图。我们可以看到，编码部分（encoders）由多层编码器(Encoder)组成（Transformer论文中使用的是6层编码器，这里的层数6并不是固定的，你也可以根据实验效果来修改层数）。同理，解码部分（decoders）也是由多层的解码器(Decoder)组成（论文里也使用了6层解码器）。每层编码器网络结构是一样的，每层解码器网络结构也是一样的。不同层编码器和解码器网络结构不共享参数。

图：6层编码和6层解码器

接下来，我们看一下单层encoder，单层encoder主要由以下两部分组成，如下图所示

Self-Attention Layer
Feed Forward Neural Network（前馈神经网络，缩写为 FFNN）

编码器的输入文本序列$w_1, w_2,…,w_n$最开始需要经过embedding转换，得到每个单词的向量表示$x_1, x_2,…,x_n$，其中$x_i \in \mathbb{R}^{d}$是维度为$d$的向量，然后所有向量经过一个Self-Attention神经网络层进行变换和信息交互得到$h_1, h_2,…h_n$，其中$h_i \in \mathbb{R}^{d}$是维度为$d$的向量。self-attention层处理一个词向量的时候，不仅会使用这个词本身的信息，也会使用句子中其他词的信息（你可以类比为：当我们翻译一个词的时候，不仅会只关注当前的词，也会关注这个词的上下文的其他词的信息）。Self-Attention层的输出会经过前馈神经网络得到新的$x_1, x_2,..,x_n$，依旧是$n$个维度为$d$的向量。这些向量将被送入下一层encoder，继续相同的操作。

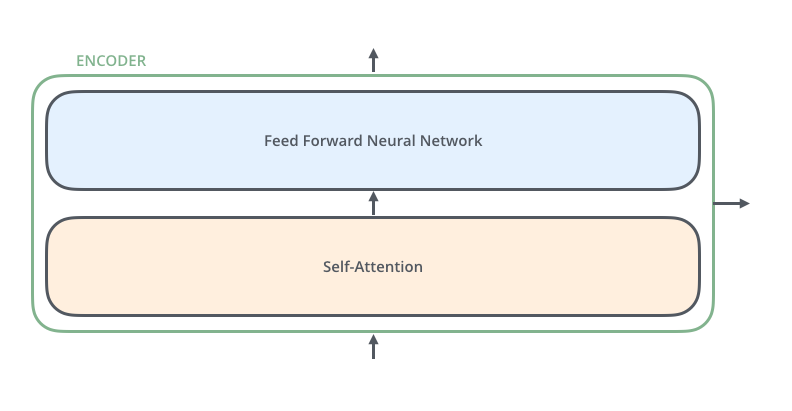
图：单层encoder

与编码器对应，如下图，解码器在编码器的self-attention和FFNN中间插入了一个Encoder-Decoder Attention层，这个层帮助解码器聚焦于输入序列最相关的部分（类似于seq2seq模型中的 Attention）。

图：单层decoder

总结一下，我们基本了解了Transformer由编码部分和解码部分组成，而编码部分和解码部分又由多个网络结构相同的编码层和解码层组成。每个编码层由self-attention和FFNN组成，每个解码层由self-attention、FFN和encoder-decoder attention组成。

以上便是Transformer的宏观结构啦，下面我们开始看宏观结构中的模型细节。

Transformer结构细节

了解了Transformer的宏观结构之后。下面，让我们来看看Transformer如何将输入文本序列转换为向量表示，又如何逐层处理这些向量表示得到最终的输出。

输入处理

词向量

和常见的NLP 任务一样，我们首先会使用词嵌入算法（embedding algorithm），将输入文本序列的每个词转换为一个词向量。实际应用中的向量一般是 256 或者 512 维。但为了简化起见，我们这里使用4维的词向量来进行讲解。

如下图所示，假设我们的输入文本是序列包含了3个词，那么每个词可以通过词嵌入算法得到一个4维向量，于是整个输入被转化成为一个向量序列。在实际应用中，我们通常会同时给模型输入多个句子，如果每个句子的长度不一样，我们会选择一个合适的长度，作为输入文本序列的最大长度：如果一个句子达不到这个长度，那么就填充先填充一个特殊的“padding”词；如果句子超出这个长度，则做截断。最大序列长度是一个超参数，通常希望越大越好，但是更长的序列往往会占用更大的训练显存/内存，因此需要在模型训练时候视情况进行决定。

图：3个词和对应的词向量

输入序列每个单词被转换成词向量表示还将加上位置向量来得到该词的最终向量表示。

位置向量

如下图所示，Transformer模型对每个输入的词向量都加上了一个位置向量。这些向量有助于确定每个单词的位置特征，或者句子中不同单词之间的距离特征。词向量加上位置向量背后的直觉是：将这些表示位置的向量添加到词向量中，得到的新向量，可以为模型提供更多有意义的信息，比如词的位置，词之间的距离等。

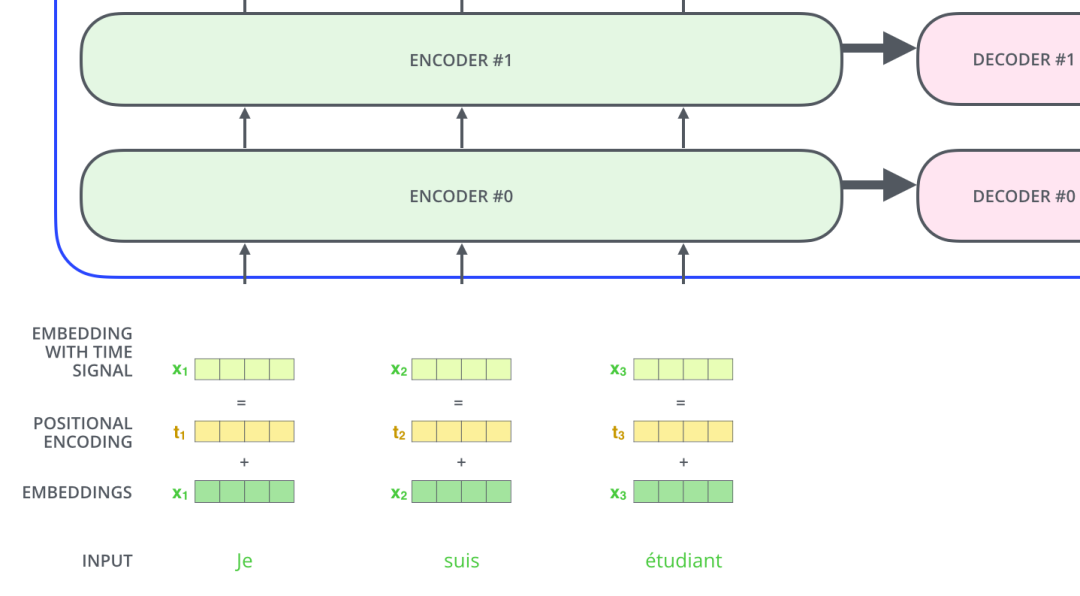
图：位置编码向量

依旧假设词向量和位置向量的维度是4，我们在下图中展示一种可能的位置向量+词向量：

图：位置编码向量

那么带有位置编码信息的向量到底遵循什么模式？原始论文中给出的设计表达式为：
$$
PE_{(pos,2i)} = sin(pos / 10000^{2i/d_{\text{model}}}) \ PE_{(pos,2i+1)} = cos(pos / 10000^{2i/d_{\text{model}}})
$$
上面表达式中的$pos$代表词的位置，$d_{model}$代表位置向量的维度，$i \in [0, d_{model})$代表位置$d_{model}$维位置向量第$i$维。于是根据上述公式，我们可以得到第$pos$位置的$d_{model}$维位置向量。在下图中，我们画出了一种位置向量在第4、5、6、7维度、不同位置的的数值大小。横坐标表示位置下标，纵坐标表示数值大小。

图：位置编码在0-100位置，在4、5、6、7维的数值图示

当然，上述公式不是唯一生成位置编码向量的方法。但这种方法的优点是：可以扩展到未知的序列长度。例如：当我们的模型需要翻译一个句子，而这个句子的长度大于训练集中所有句子的长度，这时，这种位置编码的方法也可以生成一样长的位置编码向量。

编码器encoder

编码部分的输入文本序列经过输入处理之后得到了一个向量序列，这个向量序列将被送入第1层编码器，第1层编码器输出的同样是一个向量序列，再接着送入下一层编码器：第1层编码器的输入是融合位置向量的词向量，更上层编码器的输入则是上一层编码器的输出。

下图展示了向量序列在单层encoder中的流动：融合位置信息的词向量进入self-attention层，self-attention的输出每个位置的向量再输入FFN神经网络得到每个位置的新向量。

图：单层encoder的序列向量流动

下面再看一个2个单词的例子：

图：2个单词的例子：$x_1, x_2 \to z_1, z_2 \to r_1, r_2$

Self-Attention层

下面来分析一下上图中Self-Attention层的具体机制。

Self-Attention概览

假设我们想要翻译的句子是：
$$
The \space\space animal \space\space didn’t \space\space cross \space\space the \space\space street \space\space because \space\space it \space\space was \space\space too \space\space tired
$$
这个句子中的 it 是一个指代词，那么 it 指的是什么呢？它是指 animal 还是street？这个问题对人来说，是很简单的，但是对模型来说并不是那么容易。但是，如果模型引入了Self Attention机制之后，便能够让模型把it和animal关联起来了。同样的，当模型处理句子中其他词时，Self Attention机制也可以使得模型不仅仅关注当前位置的词，还会关注句子中其他位置的相关的词，进而可以更好地理解当前位置的词。

与RNN对比一下：RNN 在处理序列中的一个词时，会考虑句子前面的词传过来的hidden state，而hidden state就包含了前面的词的信息；而Self Attention机制值得是，当前词会直接关注到自己句子中前后相关的所有词语，如下图 it 的例子：

图：一个词和其他词的attention

上图所示的it是一个真实的例子，是当Transformer在第5层编码器编码“it”时的状态，可视化之后显示it有一部分注意力集中在了“The animal”上，并且把这两个词的信息融合到了”it”中。

Self-Attention细节

先通过一个简单的例子来理解一下：什么是“self-attention自注意力机制”？假设一句话包含两个单词：Thinking Machines。自注意力的一种理解是：Thinking-Thinking，Thinking-Machines，Machines-Thinking，Machines-Machines，共$2^2$种两两attention。那么具体如何计算呢？假设Thinking、Machines这两个单词经过词向量算法得到向量是$X_1, X_2$：
$$
\begin{array}{l}
1: q_1 = X_1 W^Q, q_2 = X_2 W^Q; k_1 = X_1 W^K, k_2 = X_2 W^K\\
v_1 = X_1 W^V, v_2 = X_2 W^V, W^Q, W^K, W^K \in \mathbb{R}^{d_x \times d_k}\\
2-3: score_{11} = \frac{q_1 \cdot q_1}{\sqrt{d_k}} , score_{12} = \frac{q_1 \cdot q_2}{\sqrt{d_k}} ;\
score_{21} = \frac{q_2 \cdot q_1}{\sqrt{d_k}}, score_{22} = \frac{q_2 \cdot q_2}{\sqrt{d_k}}; \\
4: score_{11} = \frac{e^{score_{11}}}{e^{score_{11}} + e^{score_{12}}},score_{12} = \frac{e^{score_{12}}}{e^{score_{11}} + e^{score_{12}}}; \\
score_{21} = \frac{e^{score_{21}}}{e^{score_{21}} + e^{score_{22}}},score_{22} = \frac{e^{score_{22}}}{e^{score_{21}} + e^{score_{22}}} \\
5-6: z_1 = v_1 \times score_{11} + v_2 \times score_{12}; \\
z_2 = v_1 \times score_{21} + v_2 \times score_{22}
\end{array}
$$
下面，我们将上诉self-attention计算的6个步骤进行可视化。

第1步：对输入编码器的词向量进行线性变换得到：Query向量: $q_1, q_2$，Key向量: $k_1, k_2$，Value向量: $v_1, v_2$。这3个向量是词向量分别和3个参数矩阵相乘得到的，而这个矩阵也是是模型要学习的参数。

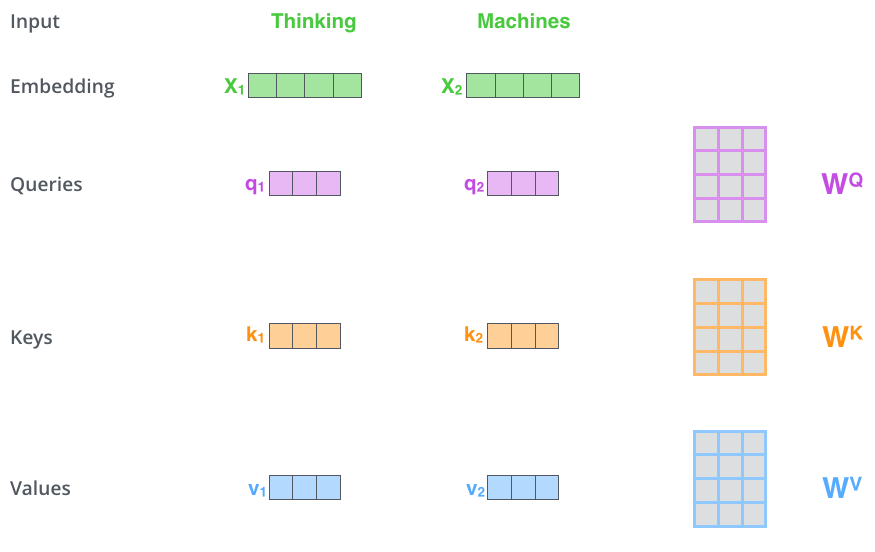图：计算Query向量：$q_1, q_2$，Key向量: $k_1, k_2$，Value向量: $v_1, v_2$。

Query 向量，Key 向量，Value 向量是什么含义呢？

其实它们就是 3 个向量，给它们加上一个名称，可以让我们更好地理解 Self-Attention 的计算过程和逻辑。attention计算的逻辑常常可以描述为：query和key计算相关或者叫attention得分，然后根据attention得分对value进行加权求和。

第2步：计算Attention Score（注意力分数）。假设我们现在计算第一个词Thinking 的Attention Score（注意力分数），需要根据Thinking 对应的词向量，对句子中的其他词向量都计算一个分数。这些分数决定了我们在编码Thinking这个词时，需要对句子中其他位置的词向量的权重。

Attention score是根据”Thinking“ 对应的 Query 向量和其他位置的每个词的 Key 向量进行点积得到的。Thinking的第一个Attention Score就是$q_1$和$k_1$的内积，第二个分数就是$q_1$和$k_2$的点积。这个计算过程在下图中进行了展示，下图里的具体得分数据是为了表达方便而自定义的。

图：Thinking的Attention Score计算

第3步：把每个分数除以 $\sqrt{d_k}$，$d_{k}$是Key向量的维度。你也可以除以其他数，除以一个数是为了在反向传播时，求梯度时更加稳定。

第4步：接着把这些分数经过一个Softmax函数，Softmax可以将分数归一化，这样使得分数都是正数并且加起来等于1，如下图所示。
这些分数决定了Thinking词向量，对其他所有位置的词向量分别有多少的注意力。

图：Thinking的Attention Score计算

第5步：得到每个词向量的分数后，将分数分别与对应的Value向量相乘。这种做法背后的直觉理解就是：对于分数高的位置，相乘后的值就越大，我们把更多的注意力放到了它们身上；对于分数低的位置，相乘后的值就越小，这些位置的词可能是相关性不大的。

第6步：把第5步得到的Value向量相加，就得到了Self Attention在当前位置（这里的例子是第1个位置）对应的输出。

最后，在下图展示了对第一个位置词向量计算Self Attention 的全过程。最终得到的当前位置（这里的例子是第一个位置）词向量会继续输入到前馈神经网络。注意：上面的6个步骤每次只能计算一个位置的输出向量，在实际的代码实现中，Self Attention的计算过程是使用矩阵快速计算的，一次就得到所有位置的输出向量。

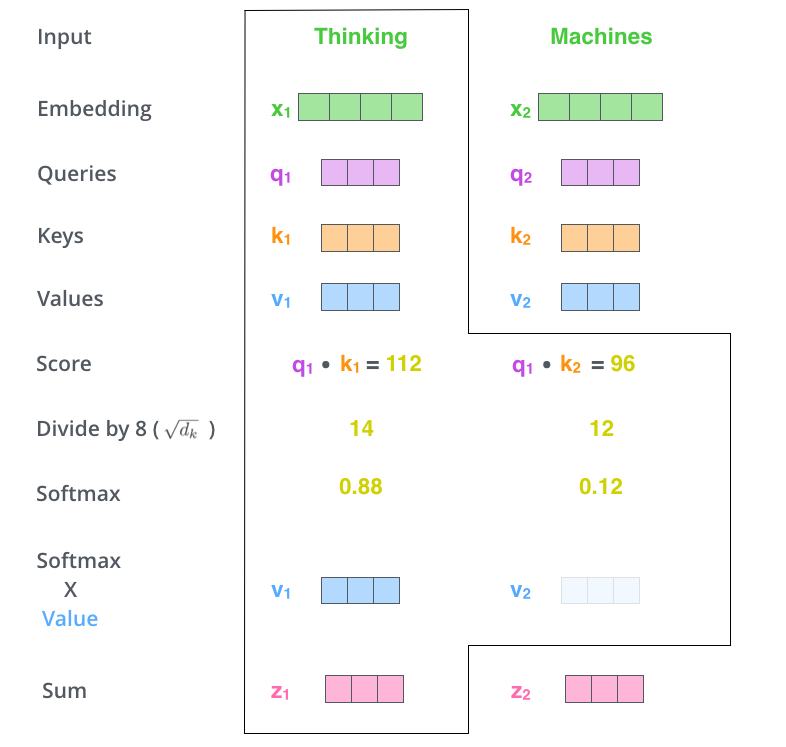
图：Thinking经过attention之后的向量表示$z_1$

Self-Attention矩阵计算

将self-attention计算6个步骤中的向量放一起，比如$X=[x_1;x_2]$，便可以进行矩阵计算啦。下面，依旧按步骤展示self-attention的矩阵计算方法。
$$
\begin{aligned}
&X = [X_1;X_2] \\
&Q = X W^Q, K = X W^K, V=X W^V \\
&Z = softmax(\frac{QK^T}{\sqrt{d_k}}) V
\end{aligned}
$$
第1步：计算 Query，Key，Value 的矩阵。首先，我们把所有词向量放到一个矩阵X中，然后分别和3个权重矩阵$W^Q, W^K W^V$ 相乘，得到 Q，K，V 矩阵。矩阵X中的每一行，表示句子中的每一个词的词向量。Q，K，V 矩阵中的每一行表示 Query向量，Key向量，Value 向量，向量维度是$d_k$。

图：QKV矩阵乘法

第2步：由于我们使用了矩阵来计算，我们可以把上面的第 2 步到第 6 步压缩为一步，直接得到 Self Attention 的输出。

图：得到输出$Z$

多头注意力机制

Transformer 的论文通过增加多头注意力机制（一组注意力称为一个 attention head），进一步完善了Self-Attention。这种机制从如下两个方面增强了attention层的能力：

它扩展了模型关注不同位置的能力。在上面的例子中，第一个位置的输出$z_1$包含了句子中其他每个位置的很小一部分信息，但$z_1$仅仅是单个向量，所以可能仅由第1个位置的信息主导了。而当我们翻译句子：The animal didn't cross the street because it was too tired时，我们不仅希望模型关注到”it”本身，还希望模型关注到”The”和“animal”，甚至关注到”tired”。这时，多头注意力机制会有帮助。
多头注意力机制赋予attention层多个“子表示空间”。下面我们会看到，多头注意力机制会有多组$W^Q, W^K W^V$ 的权重矩阵（在 Transformer 的论文中，使用了 8 组注意力),，因此可以将$X$变换到更多种子空间进行表示。接下来我们也使用8组注意力头（attention heads））。每一组注意力的权重矩阵都是随机初始化的，但经过训练之后，每一组注意力的权重$W^Q, W^K W^V$ 可以把输入的向量映射到一个对应的”子表示空间“。

图：多头注意力机制

在多头注意力机制中，我们为每组注意力设定单独的 WQ, WK, WV 参数矩阵。将输入X和每组注意力的WQ, WK, WV 相乘，得到8组 Q, K, V 矩阵。

接着，我们把每组 K, Q, V 计算得到每组的 Z 矩阵，就得到8个Z矩阵。

图：8 个 Z 矩阵

由于前馈神经网络层接收的是 1 个矩阵（其中每行的向量表示一个词），而不是 8 个矩阵，所以我们直接把8个子矩阵拼接起来得到一个大的矩阵，然后和另一个权重矩阵$W^O$相乘做一次变换，映射到前馈神经网络层所需要的维度。

图：拼接8个子矩阵并进行映射变换

总结一下就是：

把8个矩阵 {Z0,Z1…,Z7} 拼接起来
把拼接后的矩阵和WO权重矩阵相乘
得到最终的矩阵Z，这个矩阵包含了所有 attention heads（注意力头）的信息。这个矩阵会输入到FFNN (Feed Forward Neural Network)层。

以上就是多头注意力的全部内容。最后将所有内容放到一张图中：

图：多头注意力机制的矩阵运算

学习了多头注意力机制，让我们再来看下当我们前面提到的it例子，不同的attention heads （注意力头）对应的“it”attention了哪些内容。下图中的绿色和橙色线条分别表示2组不同的attentin heads：

图：it的attention

当我们编码单词”it”时，其中一个 attention head （橙色注意力头）最关注的是”the animal”，另外一个绿色 attention head 关注的是”tired”。因此在某种意义上，”it”在模型中的表示，融合了”animal”和”tire”的部分表达。

残差连接

到目前为止，我们计算得到了self-attention的输出向量。而单层encoder里后续还有两个重要的操作：残差链接、标准化。

编码器的每个子层（Self Attention 层和 FFNN）都有一个残差连接和层标准化（layer-normalization），如下图所示。

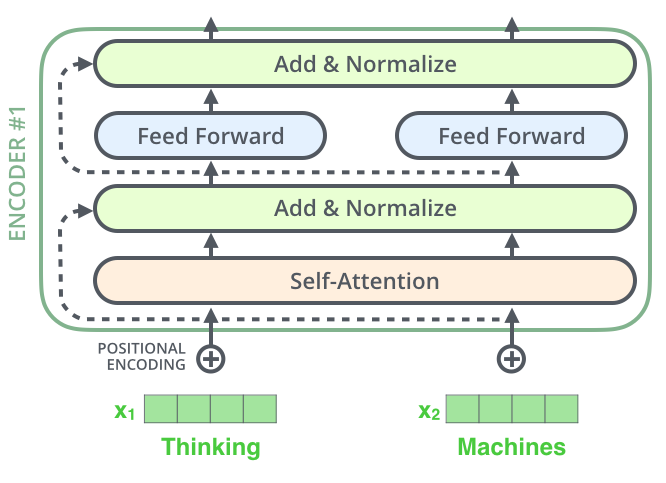
图：残差连接

将 Self-Attention 层的层标准化（layer-normalization）和涉及的向量计算细节都进行可视化，如下所示：

图：标准化细节

编码器和和解码器的子层里面都有层标准化（layer-normalization）。假设一个 Transformer 是由 2 层编码器和两层解码器组成的，将全部内部细节展示起来如下图所示。

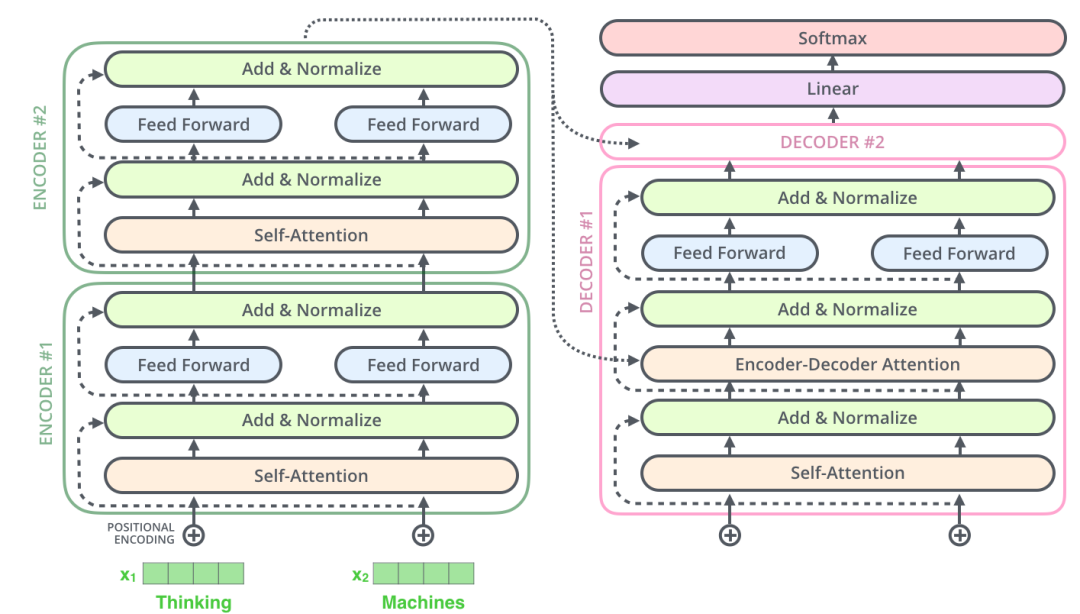
图：2层Transformer示意图

解码器

现在我们已经介绍了编码器中的大部分概念，我们也基本知道了编码器的原理。现在让我们来看下，编码器和解码器是如何协同工作的。

编码器一般有多层，第一个编码器的输入是一个序列文本，最后一个编码器输出是一组序列向量，这组序列向量会作为解码器的K、V输入，其中K=V=解码器输出的序列向量表示。这些注意力向量将会输入到每个解码器的Encoder-Decoder Attention层，这有助于解码器把注意力集中到输入序列的合适位置，如下图所示。

解码（decoding ）阶段的每一个时间步都输出一个翻译后的单词（这里的例子是英语翻译），解码器当前时间步的输出又重新作为输入Q和编码器的输出K、V共同作为下一个时间步解码器的输入。然后重复这个过程，直到输出一个结束符。如下图所示：

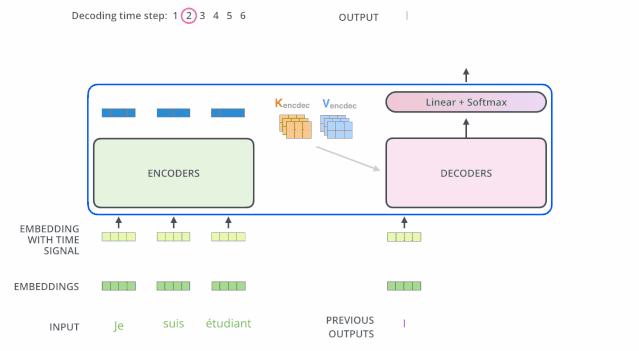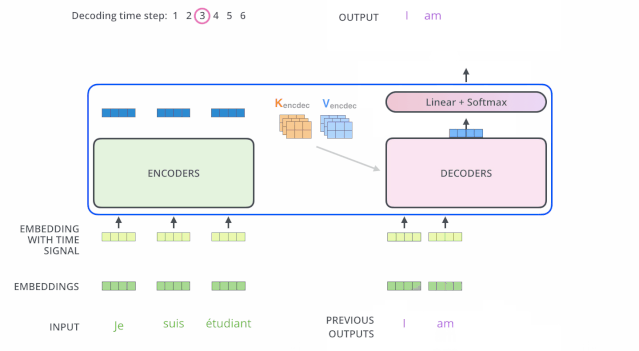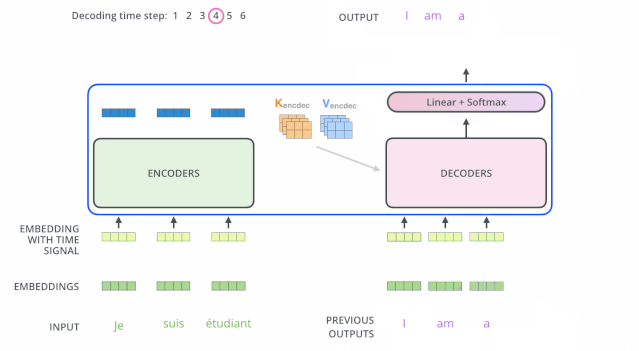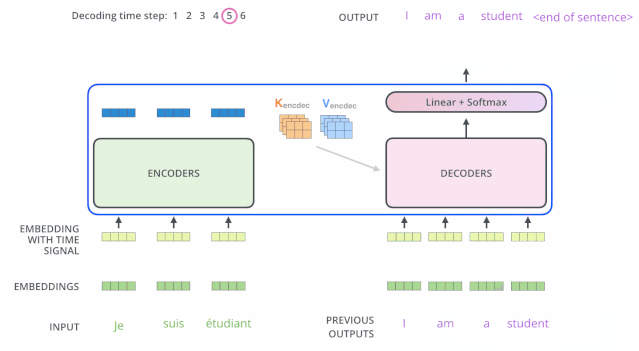
动态图：decoder动态图

解码器中的 Self Attention 层，和编码器中的 Self Attention 层的区别：

在解码器里，Self Attention 层只允许关注到输出序列中早于当前位置之前的单词。具体做法是：在 Self Attention 分数经过 Softmax 层之前，屏蔽当前位置之后的那些位置（将attention score设置成-inf）。
解码器 Attention层是使用前一层的输出来构造Query 矩阵，而Key矩阵和 Value矩阵来自于编码器最终的输出。

线性层和softmax

Decoder 最终的输出是一个向量，其中每个元素是浮点数。我们怎么把这个向量转换为单词呢？这是线性层和softmax完成的。

线性层就是一个普通的全连接神经网络，可以把解码器输出的向量，映射到一个更大的向量，这个向量称为 logits 向量：假设我们的模型有 10000 个英语单词（模型的输出词汇表），此 logits 向量便会有 10000 个数字，每个数表示一个单词的分数。

然后，Softmax 层会把这些分数转换为概率（把所有的分数转换为正数，并且加起来等于 1）。然后选择最高概率的那个数字对应的词，就是这个时间步的输出单词。

图：线性层

损失函数

Transformer训练的时候，需要将解码器的输出和label一同送入损失函数，以获得loss，最终模型根据loss进行方向传播。这一小节，我们用一个简单的例子来说明训练过程的loss计算：把“merci”翻译为“thanks”。

我们希望模型解码器最终输出的概率分布，会指向单词 ”thanks“（在“thanks”这个词的概率最高）。但是，一开始模型还没训练好，它输出的概率分布可能和我们希望的概率分布相差甚远，如下图所示，正确的概率分布应该是“thanks”单词的概率最大。但是，由于模型的参数都是随机初始化的，所示一开始模型预测所有词的概率几乎都是随机的。

图：概率分布

只要Transformer解码器预测了组概率，我们就可以把这组概率和正确的输出概率做对比，然后使用反向传播来调整模型的权重，使得输出的概率分布更加接近整数输出。

那我们要怎么比较两个概率分布呢？：我们可以简单的用两组概率向量的的空间距离作为loss（向量相减，然后求平方和，再开方），当然也可以使用交叉熵(cross-entropy)]和KL 散度(Kullback–Leibler divergence)。读者可以进一步检索阅读相关知识，损失函数的知识不在本小节展开。

由于上面仅有一个单词的例子太简单了，我们可以再看一个复杂一点的句子。句子输入是：“je suis étudiant” ，输出是：“i am a student”。这意味着，我们的transformer模型解码器要多次输出概率分布向量：

每次输出的概率分布都是一个向量，长度是 vocab_size（前面约定最大vocab size，也就是向量长度是 6，但实际中的vocab size更可能是 30000 或者 50000）
第1次输出的概率分布中，最高概率对应的单词是 “i”
第2次输出的概率分布中，最高概率对应的单词是 “am”
以此类推，直到第 5 个概率分布中，最高概率对应的单词是 “<eos>”，表示没有下一个单词了

于是我们目标的概率分布长下面这个样子：

图：目标概率分布

我们用例子中的句子训练模型，希望产生图中所示的概率分布
我们的模型在一个足够大的数据集上，经过足够长时间的训练后，希望输出的概率分布如下图所示：

图：模型训练后输出的多个概率分布

我们希望模型经过训练之后可以输出的概率分布也就对应了正确的翻译。当然，如果你要翻译的句子是训练集中的一部分，那输出的结果并不能说明什么。我们希望模型在没见过的句子上也能够准确翻译。

额外提一下greedy decoding和beam search的概念：

Greedy decoding：由于模型每个时间步只产生一个输出，我们这样看待：模型是从概率分布中选择概率最大的词，并且丢弃其他词。这种方法叫做贪婪解码（greedy decoding）。
Beam search：每个时间步保留k个最高概率的输出词，然后在下一个时间步，根据上一个时间步保留的k个词来确定当前应该保留哪k个词。假设k=2，第一个位置概率最高的两个输出的词是”I“和”a“，这两个词都保留，然后根据第一个词计算第2个位置的词的概率分布，再取出第2个位置上2个概率最高的词。对于第3个位置和第4个位置，我们也重复这个过程。这种方法称为集束搜索(beam search)。

代码实现

具体配置

我从云服务器平台租GPU来完成模型训练，以下是设备型号和CUDA版本

外部库版本如下:

导入所需包

import math
import torchtext
import torch
import torch.nn as nn
from torch import Tensor
from torch.nn.utils.rnn import pad_sequence 
from torch.utils.data import DataLoader
from collections import Counter
from torchtext.vocab import Vocab
from torch.nn import TransformerEncoder, TransformerDecoder, TransformerEncoderLayer, TransformerDecoderLayer
import io
import time 
import pandas as pd
import numpy as np
import pickle
import tqdm
import sentencepiece as spm
torch.manual_seed(0)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(torch.cuda.get_device_name(0)) 
## 如果你有GPU，请在你自己的电脑上尝试运行这一套代码

获取并行数据集

在本教程中，我们将使用从 JParaCrawl 下载的日英并行数据集二次加工后得到的数据集，由某位不知名的董老师加工后变为中日并行数据集,下面命名和en(English)有关的实际为cn(Chinese)

df = pd.read_csv('./zh-ja/zh-ja.bicleaner05.txt'
, sep='\\t', engine='python', header=None)
trainen = df[2].values.tolist()#[:10000]
trainja = df[3].values.tolist()#[:10000]
# trainen.pop(5972)
# trainja.pop(5972)
print(traincn[500])
print(trainja[500])

我们还可以使用不同的并行数据集来遵循本文，只需确保我们可以将数据处理成两个字符串列表，如上所示，包含日语和英语句子。

准备分词器

与英语或其他字母语言不同，汉语和日语句子不包含空格来分隔单词。我们可以使用JParaCrawl提供的分词器，该分词器是使用SentencePiece创建的来切分汉语和日语句子

1 2	en_tokenizer = spm.SentencePieceProcessor(model_file='enja_spm_models/spm.en.nopretok.model') ja_tokenizer = spm.SentencePieceProcessor(model_file='enja_spm_models/spm.ja.nopretok.model')

使用它们来切分句子

1	en_tokenizer.encode("All residents aged 20 to 59 years who live in Japan must enroll in public pension system.")

1	ja_tokenizer.encode("年金日本に住んでいる20歳~60歳の全ての人は、公的年金制度に加入しなければなりません。")

构建 TorchText Vocab 对象并将句子转换为 Torch 张量

使用分词器和原始句子，我们构建从 TorchText 导入的 Vocab 对象。此过程可能需要几秒钟或几分钟，具体取决于我们的数据集大小和计算能力。不同的分词器也会影响构建词汇所需的时间。

def build_vocab(sentences, tokenizer):
    """
    构建词汇表函数

    Args:
    - sentences (list): 句子列表，每个句子是一个字符串
    - tokenizer (SentencePieceProcessor): 分词器对象，用于对句子进行分词和编码

    Returns:
    - Vocab: 构建好的词汇表对象
    """
    counter = Counter()  # 创建计数器，用于统计词频
    for sentence in sentences:
        # 使用 tokenizer 对每个句子进行编码，并以字符串形式返回结果
        encoded_tokens = tokenizer.encode(sentence, out_type=str)
        # 更新计数器，统计每个子词的出现次数
        counter.update(encoded_tokens)
    
    # 创建词汇表对象，传入计数器和特殊标记
    vocab = Vocab(counter, specials=['<unk>', '<pad>', '<bos>', '<eos>'])
    
    return vocab

# 使用 build_vocab 函数构建日文和英文的词汇表
ja_vocab = build_vocab(trainja, ja_tokenizer)  # 构建日文词汇表
en_vocab = build_vocab(trainen, en_tokenizer)  # 构建英文词汇表

在有了词汇表对象之后，我们可以使用词汇表和分词器对象来构建训练数据的张量。

def data_process(ja, en):
    """
    数据处理函数，将日文和英文句子转换为张量形式

    Args:
    - ja (list): 日文句子列表
    - en (list): 英文句子列表

    Returns:
    - list: 包含日文和英文句子张量对的列表
    """
    data = []
    for (raw_ja, raw_en) in zip(ja, en):
        # 使用 ja_vocab 将日文句子转换为张量形式
        ja_tensor_ = torch.tensor([ja_vocab[token] for token in ja_tokenizer.encode(raw_ja.rstrip("\n"), out_type=str)],
                                  dtype=torch.long)
        # 使用 en_vocab 将英文句子转换为张量形式
        en_tensor_ = torch.tensor([en_vocab[token] for token in en_tokenizer.encode(raw_en.rstrip("\n"), out_type=str)],
                                  dtype=torch.long)
        # 将处理后的日文和英文句子张量对添加到 data 列表中
        data.append((ja_tensor_, en_tensor_))
    
    return data

# 使用 data_process 函数将训练数据集 trainja 和 trainen 转换为张量形式的训练数据
train_data = data_process(trainja, trainen)

创建要在训练期间迭代的 DataLoader 对象

在这里，我将BATCH_SIZE设置为 16 以防止“cuda out of memory”，但这取决于各种因素，例如您的机器内存容量、数据大小等，因此请根据需要随意更改批处理大小（注意：PyTorch 的教程使用 Multi30k 德语-英语数据集将批处理大小设置为 128。

PAD_IDX = ja_vocab['<pad>']  # 填充标记的索引
BOS_IDX = ja_vocab['<bos>']  # 句子开始标记的索引
EOS_IDX = ja_vocab['<eos>']  # 句子结束标记的索引

def generate_batch(data_batch):
    """
    生成批量数据函数

    Args:
    - data_batch (list): 包含日文和英文句子张量对的列表，每个元素为 (ja_item, en_item)

    Returns:
    - ja_batch (Tensor): 日文句子批量张量，形状为 (max_seq_len_ja, BATCH_SIZE)
    - en_batch (Tensor): 英文句子批量张量，形状为 (max_seq_len_en, BATCH_SIZE)
    """
    ja_batch, en_batch = [], []  # 初始化日文和英文批量张量列表
    for (ja_item, en_item) in data_batch:
        # 在日文句子的开头和结尾添加 <bos> 和 <eos> 标记
        ja_batch.append(torch.cat([torch.tensor([BOS_IDX]), ja_item, torch.tensor([EOS_IDX])], dim=0))
        # 在英文句子的开头和结尾添加 <bos> 和 <eos> 标记
        en_batch.append(torch.cat([torch.tensor([BOS_IDX]), en_item, torch.tensor([EOS_IDX])], dim=0))
    
    # 对日文和英文句子批量进行填充，使它们的长度一致
    ja_batch = pad_sequence(ja_batch, padding_value=PAD_IDX)
    en_batch = pad_sequence(en_batch, padding_value=PAD_IDX)
    
    return ja_batch, en_batch

# 使用 DataLoader 加载训练数据集 train_data，并生成批量数据
train_iter = DataLoader(train_data, batch_size=BATCH_SIZE,
                        shuffle=True, collate_fn=generate_batch)

Seq2seq Transformer

接下来的几个代码和文本说明（用斜体书写）取自原始的 PyTorch 教程. 除了BATCH_SIZE之外，我没有做任何更改，de_vocabwhich 这个词被改成了ja_vocab。

Transformer 是 “Attention is all you need” 论文中介绍的 Seq2Seq 模型，用于解决机器翻译任务。Transformer 模型由编码器和解码器块组成，每个块包含固定数量的层。

编码器通过一系列多头注意力和前馈网络层传播输入序列来处理输入序列。编码器的输出称为内存，与目标张量一起馈送到解码器。编码器和解码器使用教师强制技术以端到端的方式进行训练。

from torch.nn import TransformerEncoder, TransformerDecoder, TransformerEncoderLayer, TransformerDecoderLayer

class Seq2SeqTransformer(nn.Module):
    def __init__(self, num_encoder_layers: int, num_decoder_layers: int,
                 emb_size: int, src_vocab_size: int, tgt_vocab_size: int,
                 dim_feedforward:int = 512, dropout:float = 0.1):
        super(Seq2SeqTransformer, self).__init__()

        # Transformer编码器层
        encoder_layer = TransformerEncoderLayer(d_model=emb_size, nhead=NHEAD,
                                                dim_feedforward=dim_feedforward)
        self.transformer_encoder = TransformerEncoder(encoder_layer, num_layers=num_encoder_layers)

        # Transformer解码器层
        decoder_layer = TransformerDecoderLayer(d_model=emb_size, nhead=NHEAD,
                                                dim_feedforward=dim_feedforward)
        self.transformer_decoder = TransformerDecoder(decoder_layer, num_layers=num_decoder_layers)

        # 线性层，用于生成最终的目标词汇表输出
        self.generator = nn.Linear(emb_size, tgt_vocab_size)

        # 源语言和目标语言的词嵌入层
        self.src_tok_emb = TokenEmbedding(src_vocab_size, emb_size)  # TokenEmbedding是自定义的词嵌入类
        self.tgt_tok_emb = TokenEmbedding(tgt_vocab_size, emb_size)

        # 位置编码层
        self.positional_encoding = PositionalEncoding(emb_size, dropout=dropout)  # PositionalEncoding是自定义的位置编码类

    def forward(self, src: Tensor, trg: Tensor, src_mask: Tensor,
                tgt_mask: Tensor, src_padding_mask: Tensor,
                tgt_padding_mask: Tensor, memory_key_padding_mask: Tensor):
        # 对源语言和目标语言进行位置编码
        src_emb = self.positional_encoding(self.src_tok_emb(src))
        tgt_emb = self.positional_encoding(self.tgt_tok_emb(trg))

        # 编码阶段：通过Transformer编码器得到记忆(memory)
        memory = self.transformer_encoder(src_emb, src_mask, src_padding_mask)

        # 解码阶段：通过Transformer解码器生成目标语言的输出
        outs = self.transformer_decoder(tgt_emb, memory, tgt_mask, None,
                                        tgt_padding_mask, memory_key_padding_mask)
        
        # 使用线性层生成最终的目标词汇表输出
        return self.generator(outs)

    def encode(self, src: Tensor, src_mask: Tensor):
        # 编码阶段：仅使用Transformer编码器对源语言进行编码，不涉及解码
        return self.transformer_encoder(self.positional_encoding(
                            self.src_tok_emb(src)), src_mask)

    def decode(self, tgt: Tensor, memory: Tensor, tgt_mask: Tensor):
        # 解码阶段：使用Transformer解码器生成目标语言的输出
        return self.transformer_decoder(self.positional_encoding(
                          self.tgt_tok_emb(tgt)), memory,
                          tgt_mask)

文本标记通过使用标记嵌入来表示。位置编码被添加到标记嵌入中，以引入词序的概念。

class PositionalEncoding(nn.Module):
    def __init__(self, emb_size: int, dropout, maxlen: int = 5000):
        super(PositionalEncoding, self).__init__()

        # 计算位置编码矩阵
        den = torch.exp(- torch.arange(0, emb_size, 2) * math.log(10000) / emb_size)  # 计算分母
        pos = torch.arange(0, maxlen).reshape(maxlen, 1)  # 生成位置编码的位置索引
        pos_embedding = torch.zeros((maxlen, emb_size))  # 初始化位置编码矩阵
        pos_embedding[:, 0::2] = torch.sin(pos * den)  # 奇数维度上使用sin函数计算位置编码
        pos_embedding[:, 1::2] = torch.cos(pos * den)  # 偶数维度上使用cos函数计算位置编码
        pos_embedding = pos_embedding.unsqueeze(-2)  # 在倒数第二维度上添加一个维度

        self.dropout = nn.Dropout(dropout)  # 初始化Dropout层
        self.register_buffer('pos_embedding', pos_embedding)  # 注册位置编码矩阵为模型参数

    def forward(self, token_embedding: Tensor):
        """
        前向传播函数

        Args:
        - token_embedding (Tensor): 输入的词嵌入张量，形状为 (seq_len, batch_size, emb_size)。

        Returns:
        - Tensor: 添加了位置编码后的张量，形状与输入相同。
        """
        # 添加位置编码到词嵌入张量上，并应用Dropout
        return self.dropout(token_embedding +
                            self.pos_embedding[:token_embedding.size(0), :])

class TokenEmbedding(nn.Module):
    def __init__(self, vocab_size: int, emb_size):
        super(TokenEmbedding, self).__init__()
        self.embedding = nn.Embedding(vocab_size, emb_size)  # 定义词嵌入层
        self.emb_size = emb_size  # 记录词嵌入维度大小

    def forward(self, tokens: Tensor):
        """
        前向传播函数

        Args:
        - tokens (Tensor): 输入的词索引张量，形状为 (seq_len, batch_size)。

        Returns:
        - Tensor: 对应的词嵌入张量，形状为 (seq_len, batch_size, emb_size)。
        """
        # 将词索引转换为词嵌入张量，并乘以 sqrt(emb_size) 进行缩放
        return self.embedding(tokens.long()) * math.sqrt(self.emb_size)

我们创建一个后续单词掩码来阻止目标单词关注其后续单词。我们还创建掩码，用于屏蔽源和目标填充令牌

def generate_square_subsequent_mask(sz):
    """
    生成一个下三角形的mask矩阵，用于Transformer解码器中屏蔽未来信息。

    Args:
    - sz (int): 矩阵的大小，即序列长度。

    Returns:
    - torch.Tensor: 生成的mask矩阵，形状为 (sz, sz)。
    """
    mask = (torch.triu(torch.ones((sz, sz), device=device)) == 1).transpose(0, 1)  # 生成下三角形矩阵
    mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))  # 将非零位置替换为-inf，零位置替换为0.0
    return mask

def create_mask(src, tgt):
    """
    创建用于Transformer模型的掩码张量，包括源语言和目标语言的填充掩码。

    Args:
    - src (torch.Tensor): 源语言张量，形状为 (seq_len_src, batch_size)。
    - tgt (torch.Tensor): 目标语言张量，形状为 (seq_len_tgt, batch_size)。

    Returns:
    - Tuple[torch.Tensor]: 包含四个掩码张量的元组：
      - src_mask (torch.Tensor): 源语言掩码张量，形状为 (seq_len_src, seq_len_src)。
      - tgt_mask (torch.Tensor): 目标语言解码器掩码张量，形状为 (seq_len_tgt, seq_len_tgt)。
      - src_padding_mask (torch.Tensor): 源语言填充掩码张量，形状为 (batch_size, seq_len_src)。
      - tgt_padding_mask (torch.Tensor): 目标语言填充掩码张量，形状为 (batch_size, seq_len_tgt)。
    """
    src_seq_len = src.shape[0]  # 获取源语言序列长度
    tgt_seq_len = tgt.shape[0]  # 获取目标语言序列长度

    tgt_mask = generate_square_subsequent_mask(tgt_seq_len)  # 生成目标语言解码器掩码张量
    src_mask = torch.zeros((src_seq_len, src_seq_len), device=device).type(torch.bool)  # 创建源语言掩码张量，全为False

    src_padding_mask = (src == PAD_IDX).transpose(0, 1)  # 创建源语言填充掩码张量，True表示填充位置
    tgt_padding_mask = (tgt == PAD_IDX).transpose(0, 1)  # 创建目标语言填充掩码张量，True表示填充位置

    return src_mask, tgt_mask, src_padding_mask, tgt_padding_mask

当你使用自己的GPU的时候，NUM_ENCODER_LAYERS 和 NUM_DECODER_LAYERS 设置为3或者更高，NHEAD设置8，EMB_SIZE设置为512。

SRC_VOCAB_SIZE = len(ja_vocab)  # 源语言词汇表大小
TGT_VOCAB_SIZE = len(en_vocab)  # 目标语言词汇表大小
EMB_SIZE = 512  # 词嵌入维度大小
NHEAD = 8  # 注意力头数
FFN_HID_DIM = 512  # FeedForward层隐藏单元数
BATCH_SIZE = 16  # 批量大小
NUM_ENCODER_LAYERS = 3  # 编码器层数
NUM_DECODER_LAYERS = 3  # 解码器层数
NUM_EPOCHS = 16  # 训练轮数

# 初始化Transformer模型
transformer = Seq2SeqTransformer(NUM_ENCODER_LAYERS, NUM_DECODER_LAYERS,
                                 EMB_SIZE, SRC_VOCAB_SIZE, TGT_VOCAB_SIZE,
                                 FFN_HID_DIM)

# 使用Xavier初始化所有模型参数
for p in transformer.parameters():
    if p.dim() > 1:
        nn.init.xavier_uniform_(p)

transformer = transformer.to(device)  # 将模型移动到GPU上（如果可用）

loss_fn = torch.nn.CrossEntropyLoss(ignore_index=PAD_IDX)  # 定义交叉熵损失函数，忽略填充位置

optimizer = torch.optim.Adam(
    transformer.parameters(), lr=0.0001, betas=(0.9, 0.98), eps=1e-9
)  # 定义Adam优化器

def train_epoch(model, train_iter, optimizer):
    """
    训练模型一个epoch，并返回平均损失值。

    Args:
    - model (Seq2SeqTransformer): Transformer模型实例。
    - train_iter (DataLoader): 训练数据迭代器。
    - optimizer (torch.optim.Adam): 模型优化器。

    Returns:
    - float: 平均训练损失。
    """
    model.train()  # 设置模型为训练模式
    losses = 0  # 初始化损失值
    for idx, (src, tgt) in enumerate(train_iter):
        src = src.to(device)  # 将源语言数据移到GPU（如果可用）
        tgt = tgt.to(device)  # 将目标语言数据移到GPU（如果可用）

        tgt_input = tgt[:-1, :]  # 获取目标语言输入序列（不包括末尾的EOS）

        src_mask, tgt_mask, src_padding_mask, tgt_padding_mask = create_mask(src, tgt_input)  # 创建掩码张量

        logits = model(src, tgt_input, src_mask, tgt_mask,
                       src_padding_mask, tgt_padding_mask, src_padding_mask)  # 前向传播计算logits

        optimizer.zero_grad()  # 梯度清零

        tgt_out = tgt[1:, :]  # 获取目标语言输出序列（不包括开头的BOS）
        loss = loss_fn(logits.reshape(-1, logits.shape[-1]), tgt_out.reshape(-1))  # 计算损失
        loss.backward()  # 反向传播

        optimizer.step()  # 更新模型参数
        losses += loss.item()  # 累加损失值
    return losses / len(train_iter)  # 返回平均损失

def evaluate(model, val_iter):
    """
    评估模型在验证集上的性能，并返回平均损失值。

    Args:
    - model (Seq2SeqTransformer): Transformer模型实例。
    - val_iter (DataLoader): 验证数据迭代器。

    Returns:
    - float: 平均验证损失。
    """
    model.eval()  # 设置模型为评估模式
    losses = 0  # 初始化损失值
    for idx, (src, tgt) in enumerate(valid_iter):
        src = src.to(device)  # 将源语言数据移到GPU（如果可用）
        tgt = tgt.to(device)  # 将目标语言数据移到GPU（如果可用）

        tgt_input = tgt[:-1, :]  # 获取目标语言输入序列（不包括末尾的EOS）

        src_mask, tgt_mask, src_padding_mask, tgt_padding_mask = create_mask(src, tgt_input)  # 创建掩码张量

        logits = model(src, tgt_input, src_mask, tgt_mask,
                       src_padding_mask, tgt_padding_mask, src_padding_mask)  # 前向传播计算logits

        tgt_out = tgt[1:, :]  # 获取目标语言输出序列（不包括开头的BOS）
        loss = loss_fn(logits.reshape(-1, logits.shape[-1]), tgt_out.reshape(-1))  # 计算损失
        losses += loss.item()  # 累加损失值
    return losses / len(val_iter)  # 返回平均损失

开始训练

最后，在准备了必要的类和函数之后，我们准备训练我们的模型。这是不言而喻的，但完成训练所需的时间可能会有很大差异，具体取决于很多因素，例如计算能力、参数和数据集的大小。

当我使用 JParaCrawl 的完整句子列表（每种语言大约有 590 万个句子）训练模型时，使用单个 NVIDIA GeForce RTX 4090 GPU 每16个 epoch 大约需要 55分钟。

代码如下：

for epoch in tqdm.tqdm(range(1, NUM_EPOCHS+1)):
    start_time = time.time()  # 记录当前epoch开始时间
    train_loss = train_epoch(transformer, train_iter, optimizer)  # 训练一个epoch
    end_time = time.time()  # 记录当前epoch结束时间
    # 打印训练信息：当前epoch数、训练损失、当前epoch所用时间
    print((f"Epoch: {epoch}, Train loss: {train_loss:.3f}, "
           f"Epoch time = {(end_time - start_time):.3f}s"))

尝试使用经过训练的模型翻译日语句子

首先，我们创建翻译新句子的函数，包括获取日语句子、标记化、转换为张量、推理等步骤，然后将结果解码回句子，但这次是中文。

def greedy_decode(model, src, src_mask, max_len, start_symbol):
    """
    使用贪婪解码策略生成翻译结果。

    Args:
    - model (Seq2SeqTransformer): Transformer模型实例。
    - src (Tensor): 输入源语言序列张量。
    - src_mask (Tensor): 输入源语言掩码张量。
    - max_len (int): 生成的最大长度。
    - start_symbol (int): 目标语言起始符号索引。

    Returns:
    - ys (Tensor): 生成的目标语言序列张量。
    """
    src = src.to(device)
    src_mask = src_mask.to(device)
    memory = model.encode(src, src_mask)  # 编码源语言序列
    ys = torch.ones(1, 1).fill_(start_symbol).type(torch.long).to(device)  # 初始化目标语言序列起始符号
    for i in range(max_len-1):
        memory = memory.to(device)
        memory_mask = torch.zeros(ys.shape[0], memory.shape[0]).to(device).type(torch.bool)
        tgt_mask = (generate_square_subsequent_mask(ys.size(0))
                    .type(torch.bool)).to(device)
        out = model.decode(ys, memory, tgt_mask)  # 解码生成下一个目标语言单词概率分布
        out = out.transpose(0, 1)
        prob = model.generator(out[:, -1])  # 生成下一个目标语言单词的概率分布
        _, next_word = torch.max(prob, dim=1)  # 获取概率最大的单词索引
        next_word = next_word.item()  # 获取单词索引值
        ys = torch.cat([ys,
                        torch.ones(1, 1).type_as(src.data).fill_(next_word)], dim=0)  # 将预测的单词添加到目标语言序列中
        if next_word == EOS_IDX:
            break  # 如果预测的单词为结束符号，则停止生成

    return ys

def translate(model, src, src_vocab, tgt_vocab, src_tokenizer):
    """
    对源语言文本进行翻译，并返回翻译结果。

    Args:
    - model (Seq2SeqTransformer): Transformer模型实例。
    - src (str): 源语言文本。
    - src_vocab (Vocab): 源语言词汇表。
    - tgt_vocab (Vocab): 目标语言词汇表。
    - src_tokenizer (spm.SentencePieceProcessor): 源语言分词器。

    Returns:
    - str: 翻译后的目标语言文本。
    """
    model.eval()  # 设置模型为评估模式
    tokens = [BOS_IDX] + [src_vocab.stoi[tok] for tok in src_tokenizer.encode(src, out_type=str)] + [EOS_IDX]  # 将源语言文本编码为索引序列
    num_tokens = len(tokens)
    src = torch.LongTensor(tokens).reshape(num_tokens, 1)  # 将索引序列转换为Tensor，并reshape为(num_tokens, 1)
    src_mask = (torch.zeros(num_tokens, num_tokens)).type(torch.bool)  # 生成源语言掩码张量
    tgt_tokens = greedy_decode(model, src, src_mask, max_len=num_tokens + 5, start_symbol=BOS_IDX).flatten()  # 使用贪婪解码生成目标语言索引序列
    return " ".join([tgt_vocab.itos[tok] for tok in tgt_tokens]).replace("<bos>", "").replace("<eos>", "")  # 将生成的目标语言索引序列转换为文本并返回

然后，我们可以调用 translate 函数并传递所需的参数。

1
2
3

print(translate(transformer, "ライトガイドワイヤーおよびライトガイドワイヤー；", ja_vocab, en_vocab, ja_tokenizer))
print(traincn.pop(5))
print(trainja.pop(5))

保存 Vocab 对象和训练的模型

最后，在训练完成后，我们将首先使用 Pickle 保存 Vocab 对象（en_vocab 和 ja_vocab）。

import pickle
# open a file, where you want to store the data
file = open('en_vocab.pkl', 'wb')
# dump information to that file
pickle.dump(en_vocab, file)
file.close()
file = open('ja_vocab.pkl', 'wb')
pickle.dump(ja_vocab, file)
file.close()

最后，我们还可以使用 PyTorch save 和 load 函数保存模型以供以后使用。通常，有两种方法可以保存模型，具体取决于我们以后要使用它们的内容。第一个仅用于推理，我们可以稍后加载模型并使用它从日语翻译成英语。

1 2	# save model for inference torch.save(transformer.state_dict(), 'inference_model')

第二个既可以用于推理，也可以用于我们稍后想要加载模型并想要恢复训练时。

# save model + checkpoint to resume training later
torch.save({
  'epoch': NUM_EPOCHS,
  'model_state_dict': transformer.state_dict(),
  'optimizer_state_dict': optimizer.state_dict(),
  'loss': train_loss,
  }, 'model_checkpoint.tar')

加载推理模型

我们载入已经保存的模型，让它翻译日语句子

with open('en_vocab.pkl', 'rb') as file:
    en_vocab = pickle.load(file)

with open('ja_vocab.pkl', 'rb') as file:
    ja_vocab = pickle.load(file)
transformer.load_state_dict(torch.load('inference_model'))
print(translate(transformer, 
"ライトガイドワイヤーおよびライガイドワイヤー；", 
ja_vocab, en_vocab, ja_tokenizer))

Lilin

基于transformer和pytorch的中日机器翻译模型